La distanza tra due punti A e B è il segmento AB che li congiunge. Su alcuni testi viene definita come la distanza più breve per passare da un punto all’altro.
In questa lezione vedremo quindi che cos’è e come si calcola la distanza fra due punti avendone a disposizione ascisse e ordinate.
Formula distanza tra due punti
La formula generale
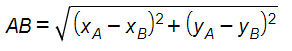
Quella che ti abbiamo appena mostrato è la formula della distanza tra due punti generici A(xA,yA) B(xB, yB) che si può applicare in qualsiasi circostanza e con qualsiasi tipo di punti.
Tuttavia ci sono alcuni casi che ci permettono di semplificare tantissimo i calcoli.
Distanza tra due punti aventi stessa ascissa
Immaginiamo di avere i due punti che hanno stessa ascissa (e quindi sono disposti lungo una retta verticale). La formula per il calcolo della della distanza tra due punti è:
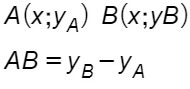
E’ sufficiente cioè fare la differenza tra le ordinate. Non è importante quale io consideri A e quale B. Il risultato sarà lo stesso.
Distanza tra due punti aventi stessa ordinata
La formula per calcolare la distanza tra due punti aventi stessa ordinata è:
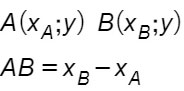
E’ sufficiente cioè fare la differenza tra le ascisse. Anche in questo caso non importa quale punto sia nella formula A e quale B, il risultato sarà lo stesso.
Dimostrazione della formula generale
Proviamo a vedere un caso concreto per la dimostrazione. Abbiamo i punti A(-5;3) e B(1;1). Il segmento AB, che nel disegno è indicato con la lettera c minuscola, è la distanza tra due punti che dobbiamo calcolare.
Si può notare, tracciando ascisse e ordinate dei due punti in modo tratteggiato che si genera un triangolo rettangolo di lati a, b, c. Dove:
- il lato a si ottiene attraverso la sottrazione yA-yB
- il lato b si ottiene attraverso la sottrazione xA-xB
- il lato c è l’ipotenusa del triangolo rettangolo (e anche la distanza tra due punti)
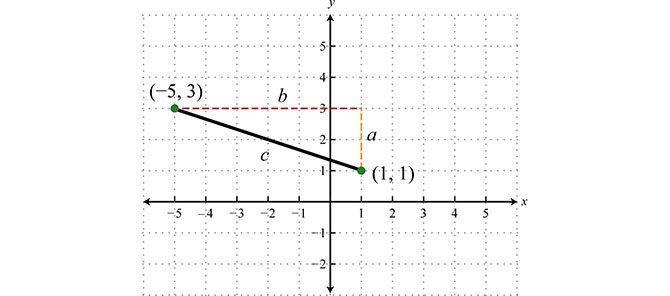
Possiamo quindi calcolare il terzo lato utilizzando la formula del teorema di Pitagora.
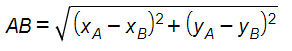
La formula per la distanza tra due punti è particolarmente semplice. Basta fissare i due punti dati dalla traccia come A e B e sostituire le rispettive coordinate nella formula vista. SI otterrà un numero, non meravigliamoci se sotto radice, che sarà la lunghezza del segmento.
Distanza tra due punti, esercizi svolti
Esercizio 1
Calcoliamo la distanza tra due punti nel piano cartesiano della seguente coppia: A(1;2) e B(1;-3/2)
Poiché i due punti hanno la stessa ascissa (x=1), allora posso applicare la formula per calcolare la distanza tra due punti aventi stessa ascissa.
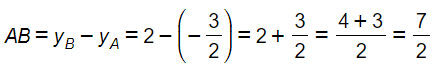
Esercizio 2:
Proviamo ora a calcolare la distanza tra i due punti nel piano cartesiano:
E(-1;+1) F(+2:+3)
Non avendo alcuna coordinata uguale, devo applicare la generica formula per il calcolare la distanza tra due punti. Per cui posso scrivere:
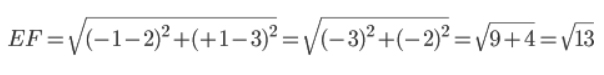
Esercizi da risolvere
Calcolare la distanza tra le seguenti coppie di punti:
A(-1;+2) B(-1;+4)
C(+5;+4) D(√2;+4)
E(+1/2;+1) F(+2;+3/2)
Si tratta di un argomento estremamente semplice per cui non è necessario dilungarsi con tanti esercizi. Si può passare direttamente al calcolo del punto medio tra due punti.
Per dubbi o chiarimenti restiamo sempre a disposizione, puoi scriverci direttamente al link contattaci.