Gli assi cartesiani sono due rette orientate che vanno a definire il piano di lavoro in geometria analitica. E’ proprio su questo sistema di riferimento cartesiano che vengono definiti gli enti geometrici fondamentali come punto e retta attraverso l’individuazione di quelle che vengono definite coordinate del punto.
Queste ci permettono l’individuazione nello spazio delle figure geometriche ed è proprio grazie agli assi cartesiani ortogonali che si individua una corrispondenza biunivoca tra gli oggetti della realtà e quelli disegnati sul tuo foglio di lavoro.
Per introdurre gli assi cartesiani
Innanzitutto cerchiamo di capire che cos’è una retta orientata:
Data una retta r è sempre possibile fissare su di essa un verso di percorrenza, che solitamente viene indicato come verso positivo.
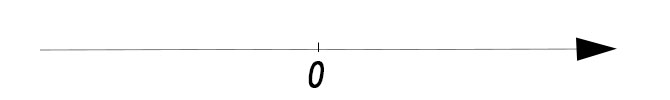
Questo significa che fissando un numero sulla retta orientata, andando nel verso della freccia si va verso numeri maggiori. Andando dall’altro senso si va verso numeri minori. Così come puoi vedere in immagine:
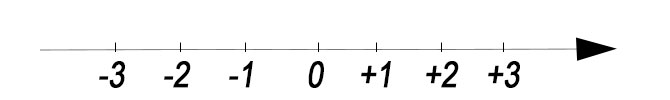
Ecco come sono indicati i numeri sugli assi cartesiani
Come si disegnano gli assi cartesiani?
Consideriamo ora due rette orientate che si intersecano perpendicolarmente nel punto O, detto origine degli assi cartesiani. In questo sistema di riferimento orientato vengono indicate con:
- x l’asse delle ascisse
- y l’asse delle ordinate
Assi cartesiani e quadranti
Come puoi vedere dalla figura in alto, siamo partiti considerando solo i valori positivi delle ascisse e delle ordinate. In realtà, volendo disegnare gli assi cartesiani completi, andremo a disegnare anche le zone negative.
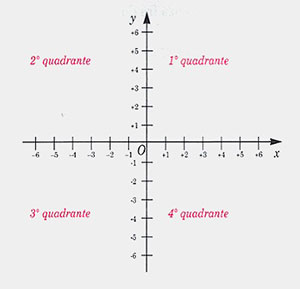
Su ogni asse cartesiano sono stati disegnati tanti valori, sia sull’asse delle x che delle y. Abbiamo cioè individuato rispettivamente il sistema ascissa e ordinata del piano.
Le rette orientate così individuate mi dividono in 4 parti il foglio di lavoro e queste sono chiamatequadranti del piano cartesiano. Per convenzione il 1° quadrante è quello in alto a destra e poi si procede in senso antiorario.
- Il primo quadrante sugli assi cartesiani è formato interamente da coppie di coordinate cartesiane positive. Qui infatti sia la x che la y sono positive.
(+ ; +) - Sul secondo quadrante invece disegneremo tutti i punti con ascisse negativa e ordinata positiva.
( – ; + ) - Sul terzo quadrante individueremo solo coordinate cartesiane negative, sia le ascisse che le ordinate ( – ; – ).
- Sul quarto quadrante invece le ascisse saranno positive e le ordinate negative ( + ; – )
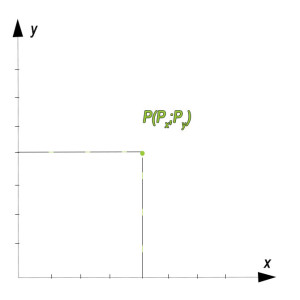
Coordinate cartesiane di un punto
Sul grafico in alto abbiamo individuato un generico punto P, le cui coordinate si indicano tra parentesi con un punto e virgola. La prima è la coordinata l‘ascissa x, cioè Px, mentre la seconda coordinata è l’ordinata y, cioè Py.
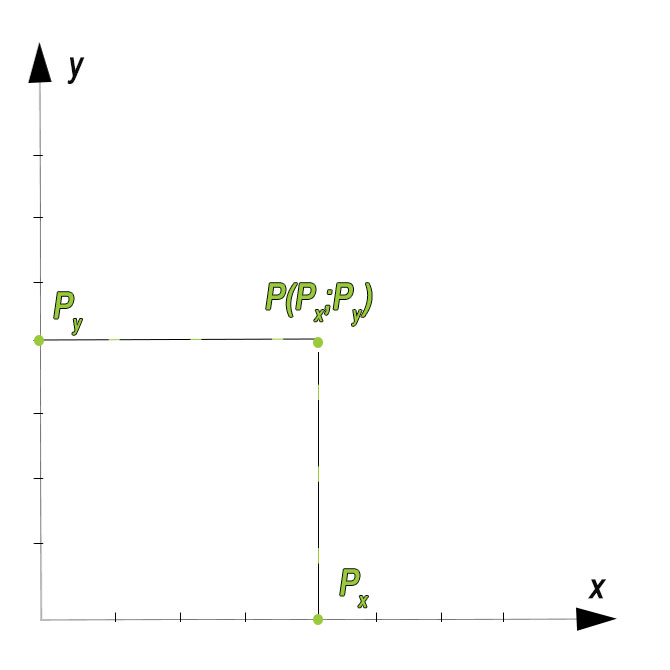
Per disegnare un punto sugli assi cartesiani in geometria analitica, sono sufficienti quindi due coordinate cartesiane, la x e la y, quindi l’ascissa e l’ordinata. La prima la posizioneremo sulla retta orizzontale, cioè sull’asse delle ascisse, mentre la seconda coordinata cartesiana la individueremo sulla retta verticale, cioè sull’asse delle ordinate.
Ovviamente si da per scontato che conosciamo il concetto di numeri relativi e quindi sappiamo benissimo la differenza tra numeri positivi o negativi. In caso contrario ti consigliamo di andare riguardarti la lezione sui numeri relativi.
Assi cartesiani esercizi svolti
Esercizio 1: Disegnare il punto partendo dalle coordinate cartesiane
Come esercizio di questa breve lezione iniziale proveremo a posizionare alcuni punti sugli assi cartesiani:
A(+1,-3)
Come detto in precedenza, in base al punto, consideriamo le due coordinate cartesiane.
Ascissa= +1
Ordinata= -3
Quindi mi sposto di “un passo” a destra e tre verso il basso. Dato infatti che la y è negativa, invece di andare verso l’alto sulla retta orientata delle ordinate, mi muoverò verso il basso. Ottengo così il punto come in figura:
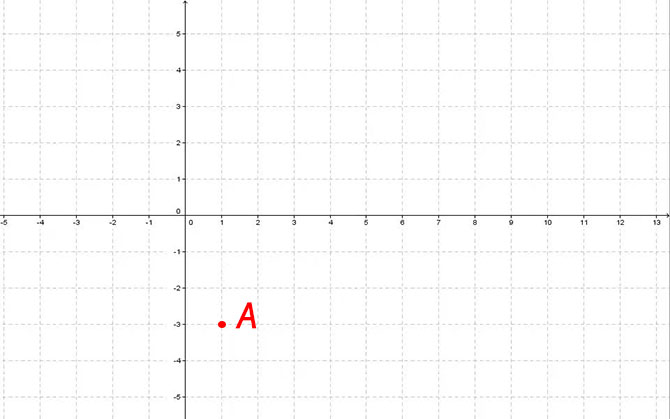
Il punto A sugli assi cartesiani
Qualsiasi siano i numeri delle ascisse e delle ordinate del punto, che siano interi, numeri relativi, radicali, eccetera, il concetto non cambia. L’ascissa va collocata sull’asse orizzontale, l’ordinata sull’asse verticale.
Piano cartesiano, esercizi da svolgere
Puoi provare tu stesso a disegnare i seguenti punti:
B (-3;-2) C (+5;0) D (-1;+1) E (+3;-3)
Come sempre restiamo a tua disposizione per dubbi, per avere gli esercizi svolti o per qualsiasi chiarimento. Se la lezione ti è stata d’aiuto ti invitiamo a lasciare un commento in basso, ci aiuterà a crescere e a migliorare la qualità delle lezioni.
Dopo questa prima lezione introduttiva sugli assi cartesiani e sulle coordinate cartesiane di geometria analitica, possiamo entrare nel cuore del programma e partire con le prime formule: distanza tra due punti e punto medio su un segmento.