Formule di addizione e sottrazione seno e coseno

Nella lezione di trigonometria di oggi vedremo quali sono le formule di addizione e sottrazione di seno e coseno. Vedremo in maniera semplice la dimostrazione e come applicare queste regole ad alcuni esempi ed esercizi svolti.

---

Cosa sono le formula di addizione e sottrazione?

Tabella con le formule complete di seno-coseno e tangente-cotangente

Formula sottrazione del coseno – dimostrazione

Formula addizione del coseno – dimostrazione

Formula addizione del seno – dimostrazione

Formula sottrazione del seno – dimostrazione

Esercizi svolti o da risolvere

---

Se stai studiando la trigonometria scoprirai presto che anche qui ci sono le operazioni algebriche come l’addizione, la sottrazione, la moltiplicazione e la divisione. Tuttavia non possono essere risolte come hai fatto finora perché esistono delle formule trigonometriche come le formule di addizione e sottrazione, le formule di duplicazione e le formule di bisezione. Nella lezione di oggi vedremo le prime con una dimostrazione che troverai molto facile.

Infatti quando ci troviamo davanti una funzione trigonometrica accade che:

Questo significa che quando hai un esercizio di trigonometria in cui c’è la somma di due angoli come argomento di un seno o di un coseno, non puoi spezzare l’addizione. Un matematico ti direbbe che il seno della somma di due angoli non equivale alla somma dei seni dei due angoli.

Vediamo con un esempio: per verificare quello che abbiamo scritto sopra possiamo prendere due valori di alfa e beta, per esempio a=30° e b=60°.

E quindi è necessario usare delle formule fondamentali per la trigonomietria.

Formule di addizione e sottrazione

Ecco lo schema in cui trovi ogni formula di addizione e sottrazione di seno e coseno.

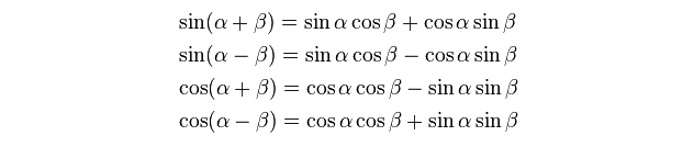
Per quanto riguarda tangente e cotangente ecco la tabella con le formule di addizione e sottrazione:

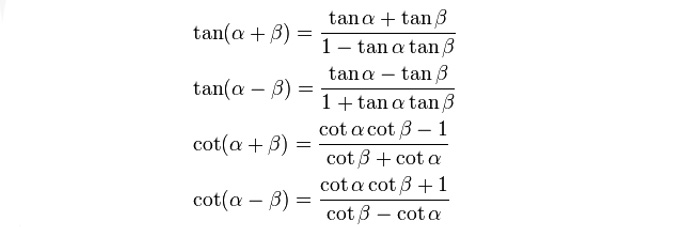
Con queste formule puoi risolvere le espressioni trigonometriche, ma se vuoi approfondire l’argomento ecco la dimostrazione della formula di addizione e sottrazione del coseno!

Dimostrazione formula sottrazione del coseno

Prendiamo una circonferenza goniometrica. Disegniamo l’angolo α nel terzo quadrante e l’angolo β nel secondo quadrante tali che la loro differenza, (α – β), sia un angolo del primo quadrante.

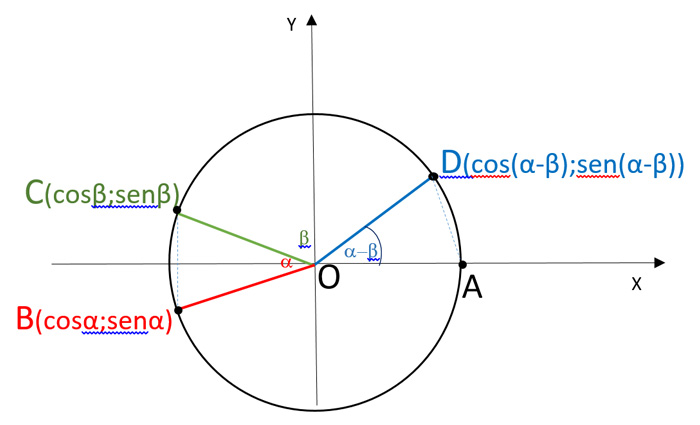
Possiamo applicare la formula della distanza tra due punti ottenendo:

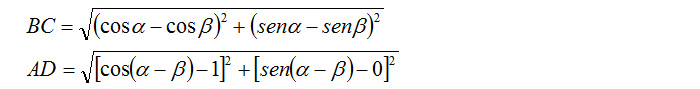 Considerando che le corde BC e AD sono uguali posso quindi impostare l’uguaglianza:

Proseguiamo con eliminando le radici quadrate elevando al quadrato primo e secondo membro e svolgiamo ogni quadrato di binomio:

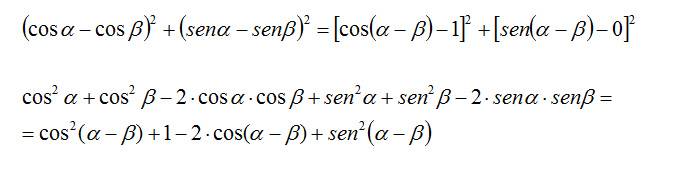
Ricordi che nelle scorse lezioni abbiamo visto le formule fondamentali della trigonometria? Abbiamo visto che il seno al quadrato più il coseno al quadrato danno sempre come risultato 1, per cui possiamo continuare a scrivere la formula di sottrazione del coseno come:

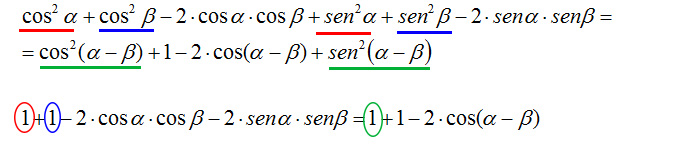
A questo punto non ci resta che fare semplificazione e facili operazioni algebriche:

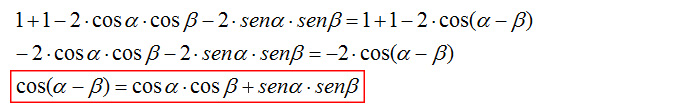
Dimostrazione formula addizione del Coseno

Per passare dalla formula di sottrazione del coseno, alla formula di addizione del coseno basta sostituire – β al posto di β. Aggiungendo il segno meno otteniamo quindi:

Dimostrazione formula addizione del seno

Si parte dalla formula di sottrazione del coseno dimostrata prima e andiamo a sostituire 90-α al posto di α e sfruttiamo gli archi associati all’interno dell’equazione trigonometrica che otteniamo:

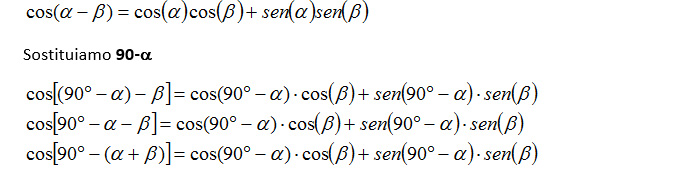
Poiché cos(90-x)=sen(x) e sen(90-x)=cos(x) allora possiamo dimostrare la formula di addizione del seno sostituendo:

Dimostrazione formula di sottrazione del seno

Partendo dall’equazione appena ottenuta, vediamo come dimostrare la regola che riguarda la sottrazione del seno. Come per la dimostrazione per la formula di addizione del coseno, sostituiamo  – β al posto di β.

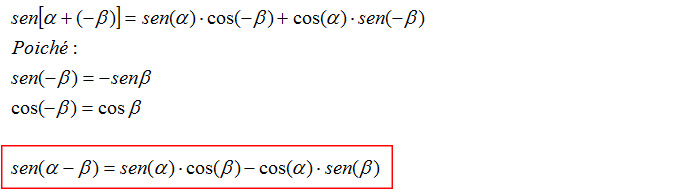
Preferiamo mantenere snella questa lezione, per cui lasciamo a te, come esercizio, la dimostrazione delle formule di addizione e sottrazione di tangente e cotangente. Il nostro suggerimento è di partire dalla definizione di tangente di un angolo (tgx=senx/cosx).

Al posto di x usa a+β e sviluppa il rapporto tra seno e coseno, usando le formula di addizione e sottrazione di seno e coseno dimostrate fino ad ora.

Esercizi svolti:

Riprendiamo l’esempio che abbiamo fatto all’inizio per cui  a = 30° e b = 60° e risolviamo la seguente espressione:

• sen(30°+60°)=

Usiamo la formula di addizione del seno:

sen(a+β)=sen(a)cos(β)+cos(a)sen(β)

sen(30°+60°)=sen(30°)cos(60°)+cos(30°)sen(60°)=

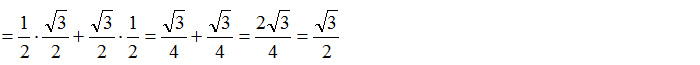
• cos(105°)=

In questo caso possiamo risolvere l’esercizio considerando che 105° = 60° + 45°.

cos(a+β)=cos(a)cos(β)-sen(a)sen(β)

cos(60°+45°)=cos(60°)cos(45°)-sen(60°)sen(45°)=

=(1/2)( √2/2)-(√3/2)(√2/2)=

=√2/4-√6/4=

(√2-√6)/4

Esercizi da risolvere

Prova a risolvere i seguenti esercizi sulle formule di addizione e sottrazione senza usare la calcolatrice.

• cos(60°+30°)
• cos(15°)
• sen(75°)

Per avere un aiuto a risolvere i tuoi compiti di trigonometria, per chiarimenti o dubbi sulla lezione di oggi, contattaci! Il nostro staff è a tua disposizione!