Come si calcola il vertice di una parabola? Quali sono le formule da usare per calcolare le coordinate del vertice? In questa lezione risponderemo a queste due domande e vedremo alcuni esercizi svolti e commentati passo passo per aiutarti a comprendere meglio l’argomento.
DEFINIZIONE: Il vertice della parabola viene definito come il punto di intersezione tra la parabola stessa e l’asse di simmetria. Nel caso di parabola ad asse verticale, il vertice diventa anche punto di minimo o punto di massimo.
Formule per il vertice della parabola
Come abbiamo visto nella spiegazione dell’equazione della parabola, possiamo avere due differenti casi: la figura ha un asse di simmetria verticale oppure orizzontale. Ciascuno dei due casi, ha un’equazione rappresentativa differente. Le formule per calcolare il vertice della parabola ovviamente dipendono anche da questi casi.
Formule vertice parabola con asse di simmetria verticale (parallelo all’asse y)
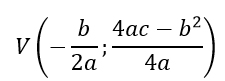
Ricordiamo che in questo caso l’equazione della parabola è:
y=ax²+bx+c
OSSERVAZIONE: ti ricordi che nel programma di algebra hai già incontrato il binomio b²-4ac ? Era la formula del DELTA che si utilizzava per risolvere le equazioni di secondo grado. Infatti le coordinate del vertice della parabola possono anche essere espresse come:
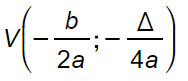
Formule vertice parabola con asse di simmetria orizzontale (parallelo all’asse x)
In questo caso le coordinate del vertice si invertono:
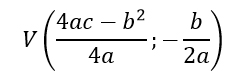
L’equazione della parabola è invece:
y=ax²+bx+c
L’osservazione fatta per il Δ continua a valere per cui, senza bisogno di ripeterci ulteriormente, possiamo dire che le coordinate del vertice di una parabola ad asse orizzontale possono essere scritte anche come:
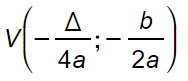
Esempi di calcolo del vertice della parabola
Determinare il vertice della parabola di equazione:
Esercizio 1
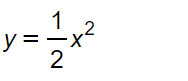
Poiché a=1/2>0, la parabola presenta la concavità rivolta verso l’alto. L’equazione è del tipo y=ax² per cui il vertice della parabola coincide con l’origine degli assi e il suo asse di simmetria coincide con l’asse delle y.
V=(0;0)
Esercizio 2
y=-x²+4
Si tratta sempre di una parabola con asse verticale, ma questa volta a=-1<0, per cui la concavità è rivolta verso il basso. Quest’ultima informazione non è rilevante per calcolare le coordinate del vertice della parabola. Una volta capita se la parabola ha asse orizzontale o verticale si può immediatamente calcolare il vertice.
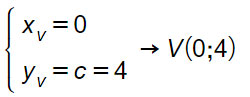
Esercizio 3
y=2x²+4x-6
La figura ha asse di simmetria verticale. Passiamo subito al calcolo del vertice della parabola.
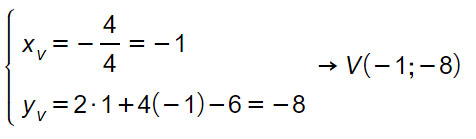
Considerazioni
Per determinare l’ordinata del vertice della parabola, in linea teorica, si può procedere in due modi:
- si usa la formula classica già vista, ovvero -Δ/4a
- poiché il vertice è un punto della parabola, dopo aver determinato la sua ascissa xv, nell’equazione della parabola si sostituisce ad x il valore di xv.
Il nostro consiglio è ovviamente di utilizzare la formula del vertice. Questo perché è vero che il secondo metodo può essere più immediato nei casi più semplici, ma usando sempre lo stesso metodo si impara prima a memoria la formula.