Abbiamo già parlato nelle scorse lezioni delle tecniche di svolgimento delle disequazioni fratte e di come queste possano facilmente essere ricondotte a delle più semplici disequazioni di primo grado.
Nella lezione di oggi faremo un piccolo passo in avanti vedendo come si svolgono le disequazioni fratte di secondo grado, analizzando degli esercizi svolti e commentati con diverso grado di difficoltà.
Come si risolvono le disequazioni di II grado fratte?
Non cambia assolutamente nulla rispetto alle disequazioni fratte di primo grado: la tecnica resta la stessa come per tutte le frazionarie. Si risolvono separatamente il pezzo di sopra (numeratore) e il pezzo di sotto (denominatore). Ecco la situazione più frequente in cui saranno espressi gli esercizi da risolvere:
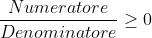
Che possiamo abbreviare per semplicità in:
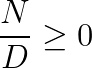
Questa si risolve, qualsiasi sia il verso della disequazione frazionaria (maggiore o minore), imponendo:
- Numeratore maggiore di zero
- Denominatore maggiore di zero
Nel caso la disequazione di secondo grado fratta abbia il maggiore e uguale o il minore e uguale, allora dovrai aggiungere il simbolo uguale SOLO AL NUMERATORE. Ricordati infatti che al denominatore non può esserci mai zero perché rende impossibile la frazione (prova a fare un numero diviso zero sulla tua calcolatrice per provare!)
Risolviamo quindi le due disequazioni separatamente e, ottenuti i risultati, si posizionano su un grafico in cui andremo a valutarne i segni.
Si prende il segno più o il segno meno?
Per trovare il risultato delle disequazioni di secondo grado fratte semplicemente si prenderà il segno corrispondente al verso della disequazione iniziale.
- Prenderai + se il verso della disequazione fratta è maggiore o maggiore e uguale
- Prenderai – se il verso della disequazione fratta è minore o minore e uguale.
Congratulazioni! Hai già completato la parte teorica di questa lezione. Ora proveremo a mettere in pratica quello che abbiamo appreso, provando a risolvere alcuni esercizi.
Esercizi disequazioni fratte di secondo grado
Esercizio 1
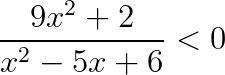
Risolviamo l’esercizio agendo separatamente su numeratore e denominatore. Quindi iniziamo a risolvere:
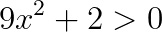
Come si può notare abbiamo messo il verso maggiore alla disequazione nonostante la traccia ci imponesse il minore. Questo perché il segno lo stabiliremo alla fine sul grafico.
Ci troviamo ad una semplice disequazione di secondo grado. Ti ricordi come si risolvono? Possiamo usare il metodo del delta oppure somma e prodotto. In questo caso, visto che manca il termine di primo grado (vedi che ci sono solo il quadrato e il termine noto?). Cosa possiamo notare?
Che 9 x alla seconda è sicuramente positivo e sommando 2, il risultato sarà ancora positivo. Quando questo numero positivo è >0? Sempre, che in linguaggio matematico si scrive “per ogni x appartenente a R”
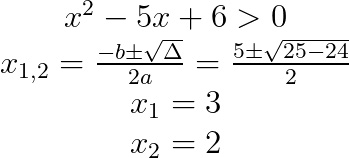
Consideriamo i valori esterni (visto che il primo coefficiente della disequazione e il suo verso sono concordi), per cui il risultato è:
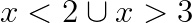
A questo punto possiamo combinare la soluzione del numeratore e del denominatore in un unico grafico. Sulla prima riga mettiamo un’unica linea continua (corrispondente al risultato “sempre”), sulla seconda riga mettiamo invece linea continua prima di 2 e dopo il 3, il resto va tratteggiato.
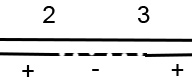
Dato che la disequazione fratta di secondo grado aveva il verso minore, il risultato sarà dato da quei valori con il segno meno. Per cui la soluzione dell’esercizio è:
2<x<3
Esercizio 2
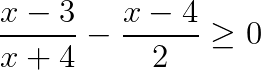
Ad un’occhiata veloce, ci si potrebbe chiedere se questo esercizio si risolva con le disequazioni fratte di secondo grado, visto che non c’è nessuna potenza. Tuttavia abbiamo una differenza di due polinomi, per cui sarà necessario eseguire il minimo comune multiplo.
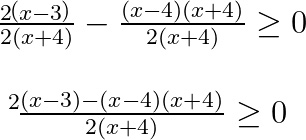
Proseguiamo sviluppando le moltiplicazioni, meglio ancora se ci ricordiamo la regola della somma di un prodotto per una differenza. Otteniamo quindi:
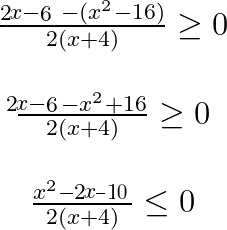
A questo punto siamo tornati al caso precedente, in cui c’è un unico numeratore e un unico denominatore, ma questa volta il verso della disequazione è minore e uguale.
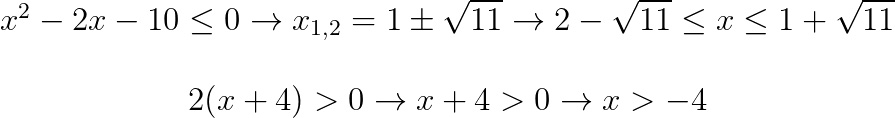
Studiamo i segni delle soluzioni su un grafico.
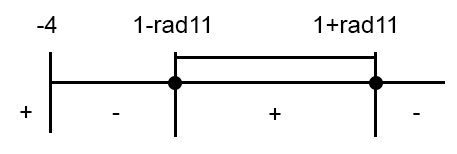
Visto che la disequazione fratta aveva il verso minore e uguale, allora prenderemo il segno meno facendo attenzione a dove c’è il segno dell’uguale – sul grafico segnato con un tondino.
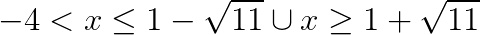
Esercizio 3
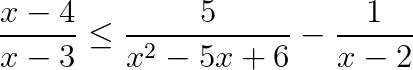
In quest’ultimo esercizio troviamo una disequazione fratta di II grado leggermente più complessa rispetto alla precedente. L’unica difficoltà, in realtà riguarda i denominatori e il calcolo del minimo comune multiplo.
Il termine centrale infatti è un polinomio di grado 2 che può essere scomposto in (x-3)(x-2). Se trovi difficoltà in questo passaggio, ti consigliamo di dare un’occhiata alla lezione sulle scomposizioni di polinomi. Il risultato che si ottiene è:
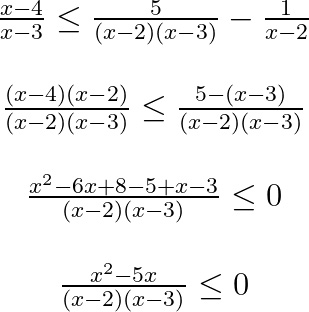
Siamo arrivati al caso N/D maggiore o minore di 0. Per cui separiamo numeratore e denominatore imponendo il primo maggiore e uguale, il secondo solo maggiore di 0. Ricorda che al denominatore non ci deve essere mai il segno uguale.
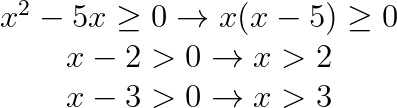
Andando a risolvere la prima, otteniamo quindi:
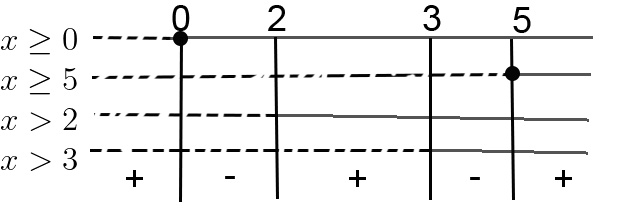
Degli intervalli indicati prenderemo i valori con il segno meno, visto che la disequazione aveva il verso minore e uguale. Quindi il risultato finale è:
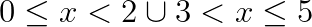
Conclusioni finali
Come hai potuto notare, le disequazioni fratte di secondo grado non sono così difficili: basta fare attenzione ai segni, saper scomporre i polinomi e calcolare correttamente il minimo comune multiplo. Non ci sono altri tipi di difficoltà.
Se questa lezione ti è stata utile o hai delle richieste per il nostro staff, lascia un commento. Ogni tuo feedback è importante per noi per crescere e per darti sempre la possibilità di lezioni aggiornate e alla portata di tutti.
Ottimo, grazie