Proprietà delle potenze, regole ed esercizi svolti

Le proprietà delle potenze sono delle regole matematiche che permettono di svolgere le principali operazioni con le potenze. Grazie a queste proprietà vengono semplificati notevolmente i calcoli, tanto che saranno spesso richiamate anche nelle equazioni letterarie, disequazioni, espressioni… Insomma trovano larga applicazione in molti tipi di esercizi, per questa ragione è importante conoscerle e soprattutto capirle bene.

Prima di partire è importante conoscere le proprietà base e le definizioni sull’elevamento a potenza. Se ti sono già note, possiamo iniziare subito con lo schema con le regole.

Quali sono le proprietà delle potenze

Molto spesso gli studenti delle scuole superiori hanno notevoli difficoltà con le regole delle potenze. Il problema maggiore non sta tanto nell’applicare le varie formule sulle proprietà delle potenze, che stiamo per vedere, ma a saperle riconoscere.

Cominciamo mostrandoti subito la tabella con le proprietà delle potenze completa, così da avere un quadro sintetico della spiegazione di oggi.

Nella tabella riassuntive che hai appena visto, sono elencate 6 regole che puoi analizzare singolarmente per eseguire le principali operazioni con le potenze. Prima di vedere nel dettaglio le regole sulle potenze, apriamo una piccola parentesi sulla questione dei segni, che spesso causa diversi errori negli esercizi di matematica.

La regola dei segni nei numeri relativi

In algebra i segni dei numeri sono fondamentali. Per evitare qualsiasi tipo di errore consigliamo di ricordare una sola semplice regola:

• esponente PARI – il segno della potenza sarà sempre positivo
• esponente DISPARI, il segno della potenza non cambia

Ad esempio, se devo risolvere una potenza negativa con indice pari, il risultato sarà sicuramente positivo.

(-5)²=+25

Se invece ho una potenza ad indice negativo, il segno meno resta.

(-5)³=-25

Proprietà delle potenze

Entriamo ora nel vivo della nostra lezione ed analizziamo le varie proprietà delle potenze, distinguendo i diversi casi a seconda delle basi e degli esponenti. Ecco le regole delle potenze da non dimenticare:

Proprietà delle potenze stessa base

Il prodotto di due potenze con la stessa base è una nuova potenza che ha per base la stessa base ed esponente la somma degli esponenti.

(-5)² x (-5)^-3 = (-5)^+2-3=(-5)^-1

Nell’esempio si nota come le due potenze, con esponenti +2 e -3, abbiano la stessa base, cioè -5. Essendoci un prodotto, si riscrive la base e si fa la somma algebrica degli esponenti, quindi si farà la somma o la differenza.

La divisione, detta anche rapporto, tra due potenze con stessa base mi dà come risultato una potenza con stessa base e differenza – cioè sottrazione – degli esponenti.

(-5)² x (-5)^-3 = (-5)^+2-(-3)=(-5)⁺⁵

In questo piccolo esercizio è possibile notare come l’unica differenza con il prodotto sta nel seno meno. Questo vuol dire che il -3 dovrà cambiare segno e diventare +3.

Proprietà delle potenze stesso esponente

La moltiplicazione tra due potenze con stesso esponente mi dà come risultato una potenza in cui la base si ottiene dalla moltiplicazione delle due basi e l’esponente non cambia.

(-3)² x (-5)² = [(-3 x (-5)]⁺²=(-15)²

Per risolvere l’esempio è stato sufficiente eseguire una banale moltiplicazione tra numeri relativi e conservare l’esponente.

Il rapporto tra due potenze con stesso esponente mi genera una nuova potenza con il rapporto delle basi e stesso esponente.

(-30)^-2 : (+5)^-2 = [(-30 : (+5)]^-2=(-6)^-2

Anche in questo caso l’esercizio si risolve in maniera molto semplice dividendo algebricamente le due basi, quindi attenzione ai segni, e mantenendo lo stesso esponente.

Potenza di potenza

La potenza di una potenza è una nuova potenza che conserva la base e per esponente ha il prodotto degli esponenti.

[(-3)² ]³ = (-3)^(+2)x(3)=(-3)⁶

Al di là della definizione che sembra complessa, risolvere le regole sulle potenze di una potenza è molto semplice. Si mette la stessa base e si moltiplicano gli esponenti.

Potenze con esponente 0

Non rientrano proprio tra le proprietà delle potenze, ma si tratta di una breve parentesi molto semplice ma che non bisogna mai dimenticare.

Qualsiasi potenza con esponente pari a 0 dà come risultato sempre +1.

(-30)⁰ = +1

Insomma non importa quale sia la base o il segno. Se l’esponente è 0, il risultato sarà sempre +1.

Potenza negativa

Se l’esponente è negativo è necessario invertire denominatore e numeratore della potenza. E se “sotto” non c’è nulla, si consideri il denominatore pari a 1. Vediamo come risolvere una potenze negative, frazioni e non, con qualche semplice esempio.

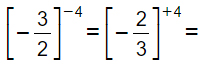
Per trasformare le potenze negative in positive, quindi basta semplicemente “capovolgere” la frazione, cioè si invertono numeratore e denominatore. In questo modo il -4 diventa +4. Nell’esempio scompare il segno meno dalla frazione perché l’esponente è pari, per cui il risultato è certamente positivo.

A questo punto non mi resta che elevare a potenza, magari aiutandomi con la calcolatrice, sia il numeratore che il denominatore ed ottengo il risultato finale.

=+16/81.

Frazioni con potenze

Non si tratta di una vera e propria regola da seguire, ma molti studenti vanno in difficoltà quando vendono un esponente su una frazione. L’unica cosa importante che non bisogna confondere è la seguente:

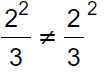
A sinistra abbiamo infatti che solo il 2 è elevato al quadrato. A destra invece c’è una frazione con la potenza ad indice 2. Ovviamene le due non vanno confuse perché nel primo caso semplicemente eleverò 2 al quadrato. Nel secondo caso bisogna elevare a potenza sia il numeratore che il denominatore.

Conclusioni

Termina così questa parte teorica sulle regole e sulle proprietà delle potenze. A questo punto non resta che iniziare a provare a risolvere degli esercizi sulle potenze. Se la lezione ti è stata utile lascia un commento qui in basso, ci aiuterai a crescere a regalarti ogni giorno nuove lezioni pensate apposta per te.

Approfondimenti: inizia a risolvere le tue prime espressioni con le potenze