Come si risolvono le potenze negative? Ho degli esercizi e delle espressioni in cui bisogna calcolare delle potenze con esponente negativo. Come mi devo comportare in questo caso? Un esercizio del tipo (-5)^(-2) come si risolve? – Grazie, Yuri
Risolvo
Le potenze con esponente negativo sono dei problemi più comuni agli studenti. Non si capisce come comportarsi di fronte ad una potenza negativa per cui in genere l’esercizio viene sbagliato. In realtà la regola da seguire è molto semplice. In questa lezione vedremo non solo, passo passo, come bisogna comportarsi di fronte ad un esponente negativo, ma vedremo anche come applicare questa regola negli esercizi con le potenze.
Potenze negative – come trasformarle
Le potenze ad esponente negativo, dette anche potenze negative, si risolvono:
eliminando il segno meno dell’esponente negativo e passando al reciproco della base
Detto in poche parole devi togliere il segno meno dall’esponente e alla base inverti numeratore e denominatore. Se il denominatore non c’è, resta sottinteso 1. Nell’esempio che il nostro studente ci ha indicato:
(-5)^(-2)=
(-1/5)^(2)
Ecco come fare:
- il numeratore 5 è diventato il denominatore della nuova base;
- il denominatore sottinteso 1 è diventato il numeratore della nuova base;
- è stato eliminato l’esponente negativo. -2 è diventato 2;
- non è stato toccato il segno meno alla base.
Nel caso più generale di potenze negative, possiamo scrivere che:
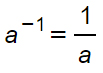
Frazione con esponente negativo
E’ il caso su cui vengono commessi più errori. Tuttavia la regola generale non cambia. L’unica differenza è che questa volta il denominatore non è sottinteso, per cui nella nuova base non avrai un numeratore pari a 1. Quando hai quindi delle frazioni con esponente negativo semplicemente ricordati di invertire numeratore e denominatore. Ad esempio:
(-5/2)^(-2)=
(-2/5)^2
Ecco come fare:
- il numeratore 5 è diventato il nuovo denominatore;
- il denominatore 2 è diventato il nuovo numeratore;
- è sparita la potenza negativa. -2 è diventato 2;
- il segno meno alla base non è stato toccato;
Possiamo quindi scrivere la regola generale valida per tutte le frazioni con esponente negativo.
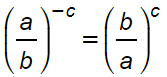
Esercizi sulle potenze con esponente negativo
Espressione 1
Possiamo risolvere immediatamente l’esercizio osservando che a e b vanno prima elevati rispettivamente a 4 e -3 e poi ancora a -2. Si tratta quindi di una potenza di potenza (vedi le proprietà delle potenze). Semplicemente moltiplichiamo gli esponenti…
![]()
La prima è una potenza negativa e va trasformata come visto nelle regole sopra, mentre la seconda resta invariata.
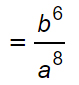
Espressione 2
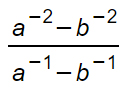
Questo secondo esercizio è un po’ più difficile degli altri perché combina frazioni positive e negative con potenze negative. Applichiamo le regole passo passo per risolverlo senza problemi…
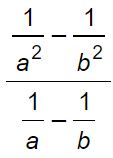
A questo punto abbiamo un numeratore e un denominatore con delle frazioni, per cui bisogna calcolare il minimo comune multiplo, sia per la frazione al numeratore (mcm:a²·b²) che per la frazione al denominatore (mcm: a·b)
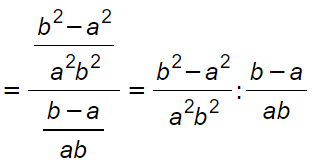
Abbiamo successivamente trasformato la linea di frazione più grande in una divisione, perché è bene ricordarlo, una frazione è pur sempre una divisione. A questo punto dell’esercizio non sono più potenze negative e possiamo trasformare la divisione in moltiplicazione invertendo numeratore e denominatore.
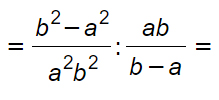
Semplifichiamo il primo denominatore con il secondo numeratore, per ottenere quindi:
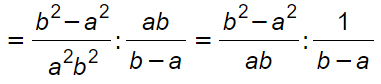
Il problema a questo punto è: come semplificare gli altri due termini? Noto che il numeratore b²-a² ha dei termini al quadrato. E’ possibile applicare una delle regole delle scomposizioni di polinomi? Si, la differenza di quadrati! Ecco quindi che l’esercizio diventa:
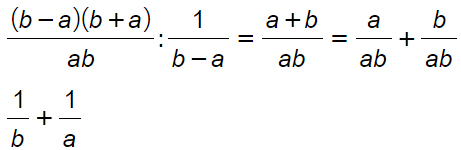
Conclusioni
Abbiamo visto quindi che per risolvere espressioni ed esercizi con potenze negative è sufficiente modificare la base nel suo reciproco. Con pochi semplici passaggi si arriva facilmente alla soluzione.
Se questa lezione ti è stata utile, l’hai trovata interessante, hai degli errori da segnalare o se hai ancora dei dubbi su degli esercizi che ti sono stati assegnati, scrivici nei commenti in basso. Aggiungeremo il tuo esercizio alla lista.