Le operazioni con i numeri relativi sono un po’ diverse da quelle studiate nel programma di aritmetica. Risolvere delle espressioni con numeri relativi significa essere in grado di fare delle somme algebriche, moltiplicazioni, divisioni e potenze.
Prima di affrontare nel dettaglio l’argomento ed analizzare le varie operazioni con numeri relativi, vedremo qualche definizione iniziale di introduzione di ripasso sui numeri relativi.
Che cosa sono i numeri relativi?
Come già detto nella lezione generale sui numeri relativi, non tutte le grandezze possono essere espresse da un numero. Basti pensare alla temperatura. Esiste una temperatura sopra lo zero e una sotto lo zero. Ad esempio d’estate si raggiungono i 30°C e d’inverno anche i -10°C. Allo stesso modo, il segno diventa un componente fondamentale in tutte le operazioni tra numeri relativi.
Esempio
-30+10 = ?
Per introdurre la somma e la differenza rivediamo due definizioni:
- si parla di numeri relativi concordi quando hanno lo stesso segno
- si parla di numeri relativi discordi quando hanno segno opposto
Le operazioni con i numeri relativi
Ti ricordi la retta orientata con i numeri negativi e positivi?
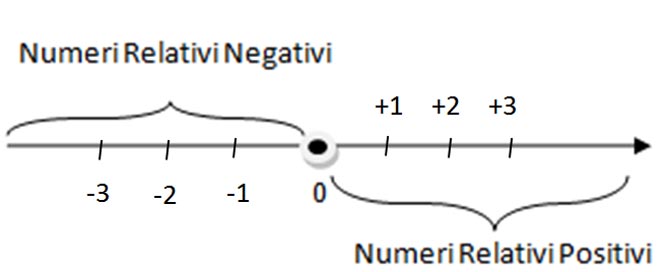
I numeri sono ordinati in senso crescente
La somma algebrica
Una volta capita la linea dei numeri relativi è tutto più facile. Distinguiamo ancora una volta i tre casi.
1 – Somma algebrica tra due numeri concordi positivi
Non cambia nulla rispetto all’addizione aritmetica. Per cui banalmente
+2+3=+5
2 – Somma algebrica tra due numeri concordi negativi
Si scrive lo stesso segno, cioè quello negativo, e si sommano i due numeri.
-7-12=-19
3 – Somma algebrica tra due numeri discordi.
Facendo finta per un attimo che i segni non esistano, si valuta il numero più grande tra i due e si tiene il suo segno. Infine si fa la differenza tra i due numeri.
Esempio:
-15+7=
Considerando solo i due numeri, cioè 7 e 15, chiaramente il numero maggiore è 15. Il suo segno è negativo, per cui il risultato della somma è negativo. Infine basta fare la differenza tra i due numeri, cioè 15-7.
Per cui il risultato è il seguente:
-15+7=-8
Altri esempi
Prova a verificare se i risultati delle seguenti addizioni sono esatte:
-10+3=-7
+15-5=+10
+23-40=-17
Sottrazione con i numeri relativi
Il discorso è perfettamente analogo con la sottrazione. La regola generale per risolvere la sottrazione con i numeri negativi è che il segno meno cambia il segno del numero.
Ad esempio:
-5-(+4)=
La parentesi è stata utilizzata perché in genere non si pongono due segni vicini senza una parentesi. Inoltre, poiché il segno meno cambia i segni degli elementi della parentesi successiva, l’equazione scritta diventa:
-5-(+4)=-5-4=
Risolvendo come già illustrato sulla somma algebrica di numeri relativi concordi negativi, ottengo
-5-(+4)=-5-4=-9
Altri esempi che puoi provare a risolvere:
-4-(-15)=-4+15=+11
+3-(-4+7-1)=+3-(+3-1)=+3-(+2)=+3-2=+1
In quest’ultimo esempio è preferibile risolvere le addizioni in parentesi, in due passaggi distinti, e poi cambiare il segno.
Per allenarti su queste piccole equazioni, consultare il testo sulle somma algebriche.
La regola dei segni con le moltiplicazioni
La regola base da tener presente è:
(+)(-)=(-)
(-)(+)=(+)
(-)(-)=(+)
(+)(+)=(+)
Nella regola dei segni basta ricordare che quando moltiplico due segni concordi il risultato è sempre positivo. Quando moltiplico due segni discordi il risultato è sempre negativo.
Per risolvere le moltiplicazioni tra numeri relativi basta infine moltiplicare i due numeri.
Ad esempio
(+3)(-5)=-15
Prova a verificare le moltiplicazioni seguenti:
(-3)(-4)=+12
(-1/2)(+3/5)=-3/10
Se hai avuto problemi con l’ultimo esercizio, prova a ripassare le operazioni con le frazioni.
Divisione tra numeri relativi
Non cambia nulla rispetto alla moltiplicazione. Si applica la regola dei segni e successivamente si esegue la divisione tra i numeri.
(-14):(-2)=+7
Ora prova tu a svolgere le divisioni tra numeri relativi seguenti:
(+40):(-4)=-10
(-32/25):(+2/5)=-16/5
Anche in questo secondo esempio, se hai avuto difficoltà ti consigliamo di rivedere gli appunti sulle frazioni.
Potenze di numeri relativi
Mentre per il numero è sufficiente semplicemente elevare a potenza, per il segno basta ricordare che:
– se l’esponente è pari, il segno è sempre positivo
– se l’esponente è dispari, il segno non cambia
Esempi:
(-4)2=+16
(-4)3=-64
Se hai riscontrato difficoltà a svolgere questi due esercizi ti consigliamo di rivedere la lezione sulle proprietà delle potenze.
La parte teorica sulla operazioni sui numeri relativi è terminata. Ti consigliamo ora di esercitarti con le espressioni algebriche con i numeri relativi. Per ulteriori dubbi o chiarimenti, lascia un commento in basso. Ci aiuterai a migliorare la qualità delle lezioni e il nostro staff sarà felice di aiutarti.