Il grafico della funzione logaritmica è uno di quegli elementi matematici da imparare a memoria, perché difficile da ricavare tramite calcoli. Ricordare però l’andamento del grafico logaritmo è importante per rispondere a tante domande immediate che potrebbero venirti chieste durante una verifica (per esempio quanto vale il logaritmo di zero o il logaritmo di infinito?)
Il grafico del logaritmo… ma quale?
Ricordi quello che abbiamo detto quando abbiamo parlato della definizione di logaritmo? Abbiamo visto che la sua forma generica è:
logab=c
dove il valore a viene definito base e può essere:
- a>1 – base maggiore di 1
- 0<a<1 – base compresa tra 0 e 1
La curva logaritmica cambia profondamente a seconda del valore della base. Ecco la ragione per cui distinguiamo due casi.
Grafico logaritmo con base maggiore di 1
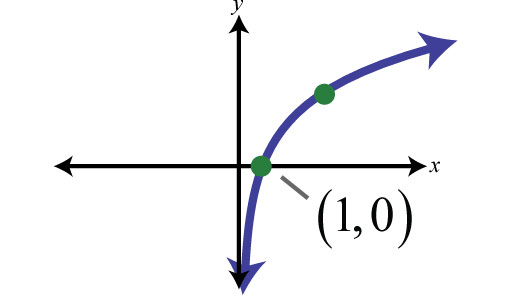
Grafico logaritmico con a>1
Le caratteristiche della curva logaritmica, con a>1, sono:
- La funzione è sempre crescente – seguendo la linea blu da sinistra verso destra, noterai che si muove sempre verso l’alto.
- Interseca l’asse x nel punto (1;0) – qualsiasi sia la base, il logaritmo di 1 vale sempre 0. Questo significa che il grafico del logaritmo tocca l’asse delle x nel punto di ascissa 1.
- Asintoto verticale in y=0 – come puoi notare osservando la linea blu, la curva del logaritmo non tocca mai l’asse delle y. Anzi quest’ultima è una retta a cui tende sempre di più senza toccare mai. E’ per questa ragione che il limite del logaritmo di zero è pari a meno infinito.
- La funzione esiste solo per x positivi – guarda il grafico. Hai notato che si sviluppa solo nel I e nel IV quadrante? Questo vuol dire che la x non assume mai valori negativi (o pari a zero). Per questa ragione si dice che l’argomento del logaritmo è sempre maggiore di 0.
- Andamento verso infinito – come puoi notare in figura in alto, il grafico del logaritmo ha un’impennata immediata dopo l’asse delle y, tocca il punto (1,0) poi continua a crescere in maniera più lente. E’ per questa ragione che il limite del logaritmo di infinito è pari a più infinito.
Grafico logaritmo con base compresa tra o e 1
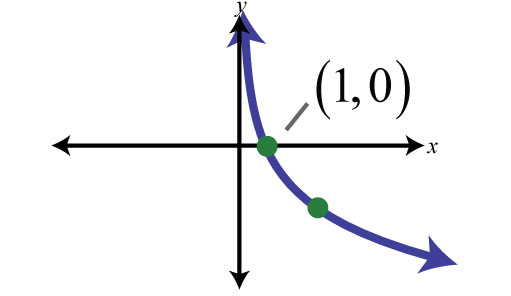
Grafico logaritmico con 0<a<1
Le caratteristiche della curva logaritmica, con 0<a<1, sono:
- La funzione è sempre decrescente – rispetto a quello che accadeva nel primo grafico, ora la funzione si muove da sinistra verso destra sempre verso il basso.
- Interseca l’asse x nel punto (1;0) – questo è l’unico aspetto in comune che hanno le due curve del logaritmo. Il punto di ascissa 1 sull’asse delle x.
- Asintoto verticale in y=0 – Anche in questo caso la funzione logaritmo ha una curva che non tocca l’asse delle y. Ma stavolta la funzione tende ad andare verso l’alto e non verso il basso. Per cui diremo, studiando poi analisi, che il limite del logaritmo quando tende a zero vale più infinito.
- La funzione esiste solo per x positivi – Anche in questo caso, la x ammette solo valori positivi visto che la funzione esiste solo nel primo e nel quarto quadrante. Quindi l’argomento del logaritmo deve essere sempre maggiore di zero.
- Andamento verso infinito – Osservando il grafico noti che la funzione ha un picco istantaneo dopo l’asse delle y, una specie di crollo verso il basso e poi tende a stabilizzarsi. Continuerà ad andare verso il basso ma in maniera più lenta. Si dirà comunque che il limite della funzione logaritmo ad infinito vale meno infinito.
In conclusione
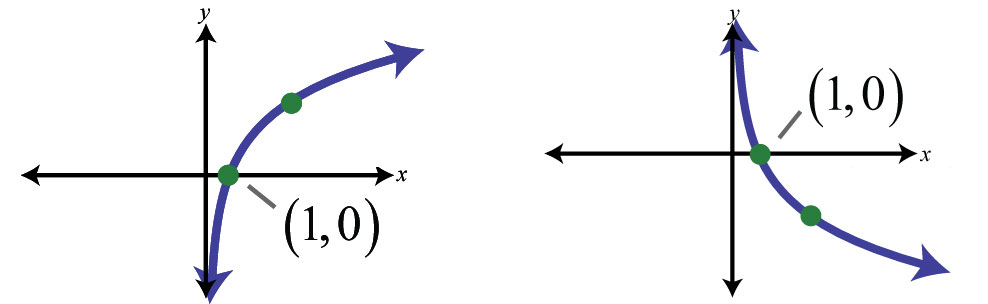
Riassumendo i contenuti di questa lezione in breve: abbiamo appreso che il grafico del logaritmo dipende dalla base utilizzata. Abbiamo distinto due casi differenti: quello in cui la base è maggiore di 1 (disegno sulla sinistra) e quello in cui la base è compresa tra o e 1. A parte alcune caratteristiche comuni, i due disegni si mostrano completamente differenti.