Le equazioni di grado superiore al secondo vengono chiamate anche equazioni scomponibili perché il procedimento risolutivo in fattori che si moltiplicano tra di loro. A questo punto semplicemente applicando la legge dell’annullamento del prodotto, che vedremo a breve, si arriva rapidamente a calcolare la soluzione.
Indice degli argomenti trattati
- Cosa sono le equazioni di grado superiore al secondo
- Legge dell’annullamento del prodotto
- Equazioni riconducibili a quelle di secondo grado
- Equazioni binomie
- Equazioni biquadratiche
- Equazioni trinomie
- Metodo di Ruffini
- Equazioni reciproche
Quali sono le equazioni di grado superiore al secondo
Sono tutte quelle equazioni in cui il grado del polinomio supera il 2. Per esempio:
x4+3x3+2x2+4x+7=0
Quella nell’esempio è un’equazione di quarto grado. Si possono risolvere utilizzando vari metodi e in alcuni testi viene esplicitamente spiegato che quando le equazioni superano il quarto grado in generale non c’è un metodo specifico risolutivo e spesso si va a tentativi.
Cosa serve sapere
Per comprendere questo argomento è importante che possegga le conoscenze di base che riguardano monomi e polinomi e soprattutto bisogna saper risolvere le equazioni di primo grado e quelle di secondo grado. Ovviamente poiché si tratta di equazioni scomponibili è importante avere una buon conoscenza delle tecniche di scomposizione dei polinomi. Se pensi di non avere grosse lacune in materia, allora possiamo iniziare.
Legge dell’annullamento del prodotto
E’ la regola fondamentale per risolvere le equazioni di grado superiore al secondo. Dati due polinomi A(x) e B(x), se abbiamo:
A(x)·B(x)=0
allora questa si può risolvere come:
A(x)=0 V B(x)=0
Quindi riassumendo se abbiamo un moltiplicazione di polinomi con al secondo membro lo zero, si risolve ponendo ogni fattore uguale a zero. Per esempio:
(3x-2)(4x+1)=0
3x-2=0 → x=2/3
4x+1=0 → x=-1/4
Equazioni riconducibili a quelle di secondo grado
Vediamo alcuni casi in cui queste equazioni sono scomponibili semplicemente attraverso un raccoglimento a fattor comune totale o parziale.
Caso 1: Manca il termine noto
Nel caso in cui nell’equazione di terzo grado manchi il termine noto, cioè il numero senza la x, è sufficiente effettuare un raccoglimento totale della x stessa. Si mette cioè la x in evidenza e si ottengono due fattori, cioè due parentesi che si moltiplicano e sono uguali a zero. Applicando la legge dell’annullamento del prodotto si ottiene come prima soluzione immediata che x=0 mentre le altre due soluzioni si ottengono con la formula risolutiva delle equazioni di secondo grado. Per esempio:
x3+4x2-5x=0
x(x2+4x-5)=0
x=0
x2+4x-5=0 → Calcolo il delta → Δ=b2-4ac=16-4(1)(+5)=16+20=36
x=(-4±√36)/2
x=-5
x=1
Caso 2: ci sono termini “simili”
Quando nell’equazione di terzo grado noti la presenza di monomi con gli stessi coefficienti, allora puoi provare ad eseguire una scomposizione attraverso un raccoglimento parziale. In questo modo ottieni due parentesi che si moltiplicano, per cui come nei casi precedenti arrivi rapidamente alla soluzione. Per esempio:
3x3+4x2-3x-4=0
3x(x2-1)+4(x2-1)=0
(x2-1)(3x+4)=0
Equazioni monomie
Sono in assoluto le più facili equazioni di grado superiore al secondo. Si presentano nella forma:
axn=b
Le possibilità a questo punto sono 2:
CASO 1: n pari
Se il grado del polinomio è pari, allora dovrai assicurarti che il secondo termine (cioè la b) sia maggiore e uguale di 0. Altrimenti otterresti un’equazione impossibile da risolvere nel campo dei numeri reali. Con b≥0, allora si risolve con la radice ennesima di entrambi i membri e aggiungendo il simbolo ± (non dimenticarlo, altrimenti l’esercizio è incompleto).
x=±n√(b/a)
CASO 2: n dispari
Se l’equazione di grado superiore al secondo ha indice dispari, quindi è alla terza o alla quinta, allora si risolve come il caso precedente ma non ci sono condizioni alla b. Può essere sia positiva che negativa. Inoltre nel risultato finale non bisogna più mettere il ±. Per cui:
x=n√(b/a)
Equazioni biquadratiche
Si tratta di equazioni di quarto grado in cui non ci sono il monomio di terzo e di primo grado. Si presenta cioè nella forma:
ax4+bx2+c=0
Quell che si nota è che, semplicemente effettuando una sostituzione y=x2, ti riconduci facilmente alle equazioni di secondo grado. Facciamo un esempio pratico:
x4 – 5x2 + 4 = 0
x2 =y
y2 – 5y + 4 = 0 → y=+4 V y=+1
A questo punto una volta trovata la variabile y bisogna sostituire e tornare alla x.
x2 =1 → x=±1
x2 =4 → x=±2
Per altri esercizi ed appunti ti invitiamo a leggere la lezione specifica sulle equazioni biquadratiche.
Equazioni trinomie
Il caso è del tutto analogo alle equazioni biquadratiche, cambia solo la sostituzione da eseguire. In questo caso la forma trovata è:
ax6+bx3+c=0
E’ un’equazione di sesto grado ma proviamo a considerare y=x3. Allora l’equazione diventa:
ay2+by+c=0
A questo punto risolviamo l’equazione di secondo grado calcolando le soluzioni in y, poi si sostituisce di nuovo come fatto con le biquadratiche. Per approfondimenti, esempi ed esercizi svolti vai alla lezione sulle equazioni trinomie.
Metodo di Ruffini
In questa lezione faremo solo un breve accenno a questa regola, visto che abbiamo deciso di dedicarvi una lezione specifica. Per approfondimenti, infatti, ti rimandiamo ai nostri appunti sulla regola di Ruffini per la divisione di polinomi. In maniera molto sintetica, data un’equazione di grado superiore al secondo:
axn+bxn-1+ … +c=0
Si vanno ad analizzare i sottomultipli di c e si verifica quali di questi rappresentano uno zero del polinomio. Cosa vuol dire? Facciamo un esempio pratico:
x3-x+6=0
E’ un’equazione di terzo grado dove il termine noto è 6. I suoi sottomultipli sono ±1 ±3 ±2 ±6. Se provo a sostituire uno di questi al posto della x mi esce 0=0. Quali di questi? Si va per tentativi:
- se sostituisco x=1 → 13-1+6=0 →6=0 → Non va bene, andiamo avanti.
- se sostituisco x=2 → 23-2+6=0 → 8-2+6=0 →12=0 → Non va bene, andiamo avanti.
- se sostituisco x=-2 → (-2)3-(-2)+6=0 → -8+2+6=0 → 0=0 VA BENE.
x=-2 è uno zero del polinomio, quindi è la prima soluzione dell’equazione di grado superiore al secondo. La inseriamo nello schema del metodo di Ruffini.
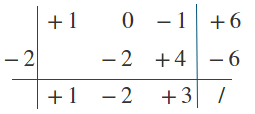
Da notare come al posto del termine al quadrato, che manca nell’equazione di terzo grado della traccia, abbiamo inserito uno 0 nel primo rigo. Se non ti è chiaro come è stato svolto il calcolo il tabella, da un’occhiata veloce alla lezione sul metodo di Ruffini.
A questo punto abbiamo scomposto il polinomio da: x3-x+6=0 2 → (x+2)(x2-2x+3)=0
Ci siamo ricondotti ai casi precedenti, per cui si applica la legge dell’annullamento del prodotto e si arriva rapidamente alla soluzione.
Equazioni reciproche
Meritano un discorso di approfondimento le equazioni reciproche, così definite perché hanno dei coefficienti uguali (o opposti). La definizione dice che un’equazione reciproca è un’equazione di grado superiore al secondo in cui sono uguali o opposti i coefficienti equidistanti dal centro dell’equazione. Cioè si presenta nella formula:
ax3+bx2+bx+a=0 oppure ax3-bx2+bx-a=0
Se si tratta di un’equazione di terzo grado, come nella forma generica che ti abbiamo mostrato, allora sicuramente l’equazione è divisibile per x=1 (se i coefficienti sono opposti) oppure per x=-1 (se i coefficienti sono uguali). Quindi possiamo risolvere immediatamente con Ruffini. Nel caso in cui ci sia da risolvere un equazione di quarto grado, non è detto che ciò sia vero, per cui è consigliabile procedere seguendo in maniera rigorosa il metodo di Ruffini.
In realtà ci sarebbe un metodo alternativo, forse un po’ più laborioso per risolverle, ma per quello vi rimandiamo alla lezione di approfondimento sulle equazioni reciproche.