L’equazione della circonferenza in geometria analitica può essere espressa in due diversi modi. Per determinarla in maniera univoca servono necessariamente 3 dati, perché proprio 3 sono le incognite di questa equazione. In questa lezione vedremo tutto quello che c’è da sapere sulla formula dell’equazione della circonferenza. Metteremo infine in pratica quanto appreso attraverso degli esempi svolti e degli esercizi commentati e con soluzione.
Ovviamente prima di partire con la formula della circonferenza, è necessario fare un brevissimo richiamo su questa figura geometrica. Dagli studi delle scuole inferiori è noto che, per definizione:
La circonferenza per definizione è il luogo geometrico dei punti equidistanti dal centro.
Questo significa che tutti i punti della circonferenza hanno la stessa distanza dal centro e tale distanza si chiama raggio. Il centro e il raggio sono proprio i due punti più importanti di questa figura anche in geometria analitica.
Equazione circonferenza
![]()
![]()
dove:
- α, β sono le coordinate del centro C;
- r è il raggio della circonferenza;
- a, b, c sono tre coefficienti che influenza posizione e dimensione della circonferenza.
Quale equazione della circonferenza bisogna usare?
Generalmente la prima equazione viene usata quando si conoscono il centro e il raggio. La seconda equazione si usa invece in tutti gli altri casi, come per esempio l’appartenenza di un punto alla circonferenza, la condizione di tangenza con una retta o un’altra qualsiasi curva…
Approfondimenti: tabella riepilogativa con tutte le formule sulla circonferenza
Le formule per trovare raggio e centro
Mentre nella prima equazione il centro e il raggio si trovano anche a occhio visto che sono esplicitati, nell’equazione generale della circonferenza servono le due seguenti formule:
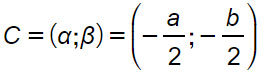
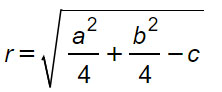
Con le ultime due formule puoi calcolare centro e raggio qualsiasi sia l’equazione generica della circonferenza. Ti saranno quindi molto utili nello svolgimento degli esercizi.
Dimostrazione dell’equazione della circonferenza
Abbiamo detto che la distanza di un generico punto P di coordinate generiche x e y dal centro C di coordinate α e ß (alfa e beta) deve essere pari al raggio. Quindi i nostri dati sono:
- P(x;y) – punto generico che appartiene alla circonferenza
- C(α;ß) – centro della circonferenza
- r – raggio della circonferenza
Calcolo la distanza tra due punti PC e la impongo pari al raggio.

A questo punto sviluppo il quadrato di binomio presente nelle due parentesi per ottenere il seguente svolgimento.
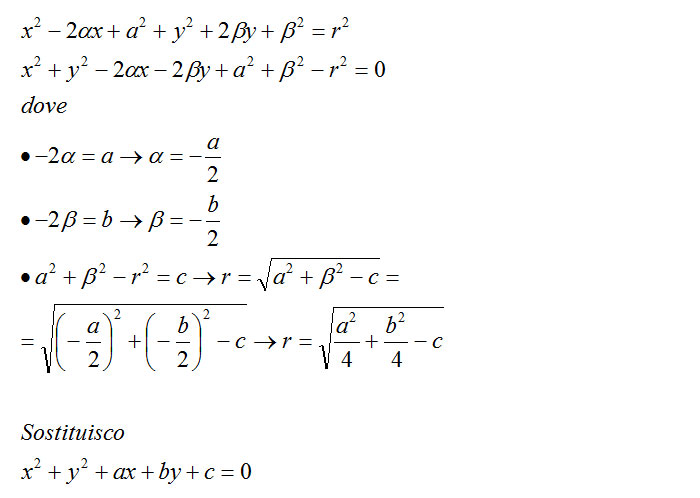
Quella che vedi è l’equazione circonferenza generale, formula molto importante da ricordare e da cui poi ricavare raggio e centro grazie alla tabella che stai per vedere.
Equazione circonferenza, caratteristiche
Una domanda che spesso crea problemi agli studenti è come riconoscere l’equazione della circonferenza? Cioè come si fa a stabilire se un’equazione rappresenta una circonferenza oppure un’altra generica curva? Le condizioni che devono verificarsi sono le seguenti:
- l’equazione è di 2° grado, sia nell’incognita x che y
- PROBLEMA DI VERIFICA: prova a calcolare il raggio della circonferenza. Se è uguale a 0 oppure minore di 0, certamente non si tratta di una circonferenza! (utilizza questo criterio in tutti gli esercizi in cui ti viene chiesto di verificare se una determinata equazione è una circonferenza)
- Infine guarda i coefficienti dei termini di secondo grado. Devono essere uguali, altrimenti potresti essere di fronte all’equazione dell’iperbole o dell’ellisse.
A questo punto analizziamo assieme quelli che sono i casi più ricorrenti e le difficoltà più frequenti nel risolvere gli esercizi sulla circonferenza.
Esercizi sull’equazione della circonferenza
Esercizio 1
Determinare l’equazione della circonferenza di centro C(0;0) e r=2.
(x-α)²+(y-β)²=r²
C=(α;β)=(0;0)
r=2
(x-0)²+(y-0)²=2²
x²+y²=4
Esercizio 2
Determinare l’equazione della circonferenza di centro C(0;3) e raggio=2.
(x-α)²+(y-β)²=r²
C=(α;β)=(0;3)
r=2
(x-0)²+(y-3)²=2²
x²+y²-6y+9=4 → Portiamo tutti i termini noti al primo membro
x²+y²-6y+9-4=0
x²+y²-6y+5=0
Esercizio 3
Stabiliamo quali delle seguenti equazioni rappresentano una circonferenza e in caso affermativo determinare centro e raggio.
a) x²+y²-2x+3y+4=0
Verifica 1: i coefficienti dei termini di secondo grado sono uguali.
Verifica 2: verificare che il raggio sia maggiore di 0.
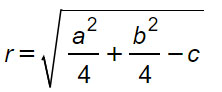
r=√(1+9/4-4) <0 NON E’ UNA CIRCONFERENZA
b) x²+y²+√2x-4y-5=0
Verifica 1: anche in questo caso i coefficienti di x² e y² sono identici (cioè pari a 1)
Verifica 2: il raggio deve essere maggiore di zero.
a²/4 + b²/4 – c = 1/2 +4 + 5 = 19/2 >0 → L’equazione rappresenta una circonferenza
Il centro è: C(-a/2;-b/2)=(-√2/2;2)
Il raggio è: r=√(19/2)=(√38)/2
Nell’ultimo passaggio è stata eseguita una razionalizzazione dei radicali.
c) x²+y²-2x-6y+10=0
Poiché a²/4 + b²/4 – c = 1 + 9 – 10 = 0, l’equazione è soddisfatta unicamente da x=1 e y=3. In poche parole significa che la circonferenza di raggio 0 non è altro che un punto. Per cui NON è una circonferenza.
Esercizio 4
Determiniamo per quali valori di k, l’equazione x²+y²+2x-6y+k=0 rappresenta una circonferenza.
Deve essere a²/4 + b²/4 – c >0
Quindi:
1-9-k>0
E’ una disequazione di primo grado molto facile da risolvere.
k<10
Ottima spiegazione dei passaggi !,,,