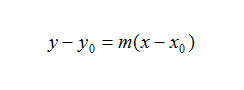Il fascio di rette è un insieme di rette tra loro parallele o incidenti. In questa lezione, oltre alle definizioni preliminari, vedremo anche una spiegazione completa su come riconoscerle e su come risolvere gli esercizi con degli esempi svolti. Vedremo ad esempio come trovare il fascio di rette per un punto o come trovare il centro del fascio.
Per affrontare questo argomento è necessario che alcuni concetti studiati nel programma di geometria analitica siano già ben noti. Nelle precedenti lezioni abbiamo parlato delle formule delle rette parallele e perpendicolari. Si tratta di una conoscenza preliminare importante perché per parlare di fascio di rette propri e impropri bisogna sapere almeno cosa sono due rette parallele.
Ma prima è necessario dare la definizione di punto proprio e punto improprio.
Premessa per distinguere il fascio proprio e improprio
Il punto proprio non è altro che il punto geometrico a cui siamo stati abituati sin dalla geometria elementare, per cui non ci dilunghiamo nella sua spiegazione. Il punto improprio per definizione è invece il punto che va all’infinito. Non lo vediamo sulla carte perché si trova in una posizione lontanissima, irraggiungibile. Le rette parallele le abbiamo definite come rette che non si incontrano mai. In realtà nei programmi universitari di disegno, si dice che esse in realtà si incontrano nel punto improprio. Per cui riepilogando:
- il fascio di rette proprio → è un insieme di rette che hanno un unico punto in comune.
- il fascio di rette improprio → è un insieme di rette parallele.
Il fascio di rette proprio
Il fascio proprio di rette per definizione è un insieme di rette che si intersecano in un unico punto proprio.
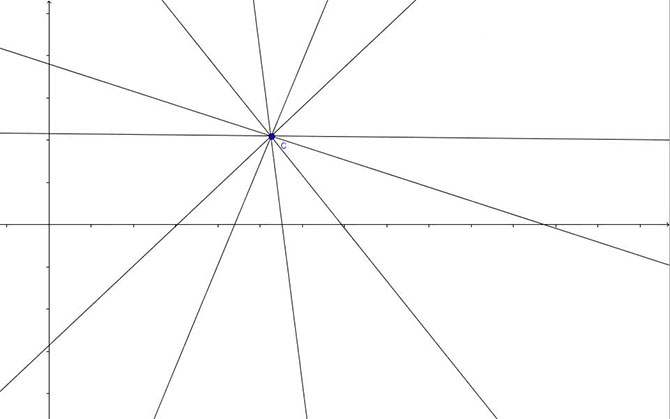
Fascio di rette proprio
Il punto in comune a tutte le rette C si chiama Centro del Fascio. Il fascio di rette proprio nel piano cartesiano si studia ricordando la formula di una retta passante per un punto e di coefficiente angolare dato.
Infatti tutte le rette del fascio proprio passano per un punto ( il centro del fascio) e di variabile hanno solo l’inclinazione, che in geometria analitica si rappresenta con il coefficiente angolare m.
Esiste una diversa formula per il fascio proprio, che si basa sulle rette generatrici:
(ax+by+c)+k(a’x+b’y+c)=0.
Si tratta di una combinazione lineare delle rette generatrici e per trovare il centro basta mettere a sistema le rette delle equazioni del fascio proprio.
Il fascio di rette improprio
Per definizione il fascio di rette improprio è l’insieme di tutte le rette parallele ad una data retta data.
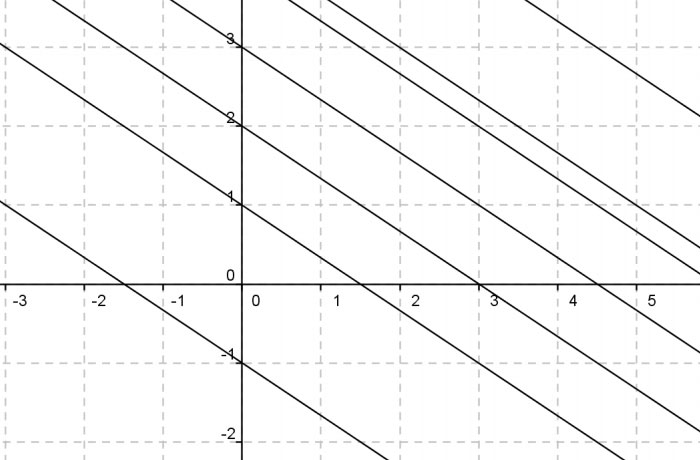
Fascio di rette improprio
Il coefficiente angolare m si suppone fisso, dato che tutte le rette del fascio improprio hanno la stessa inclinazione. Il termine noto q dell’equazione della retta deve necessariamente variare. L’equazione di un fascio di rette improprio è quindi:
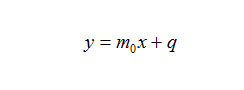
Equazione del fascio di rette improprio
Una volta capito che cos’è un fascio improprio o un fascio proprio di rette e quali sono le equazioni che regolano le figure studiate, la parte teorica è praticamente finita. Vi mostriamo ora un paio di esercizi svolti piuttosto semplici…
[adrotate banner=”4″]
Fascio di rette – esercizi svolti
Esercizio 1
Dato il fascio di rette improprie con retta base r:x+3y=0, troviamo l’equazione della retta del fascio passante per P(-2,-1).
Quello che ci sta chiedendo l’esercizio è di trovare il fascio di rette per un punto. Iniziamo calcolando il coefficiente angolare della retta:
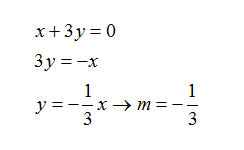
Calcoliamo il coefficiente angolare della retta del fascio improprio
A questo punto posso scrivere già l’equazione del fascio improprio di rette. m infatti è fisso mentre q possiamo lasciarlo come lettera, dato che è variabile:
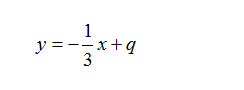
Equazione del fascio improprio di rette
Imponiamo ora l’appartenenza del punto P(-2:-1) al fascio improprio. Cioè sostituiamo le coordinate del punto nell’equazione del fascio.
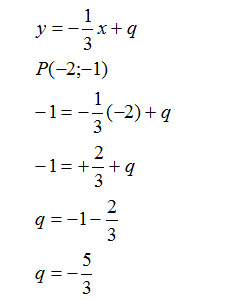
Esercizio 2
Date le rette di equazione r:x+y+1=0 e s:2x-y=0, queste generano un fascio proprio. Determinare il centro del fascio.
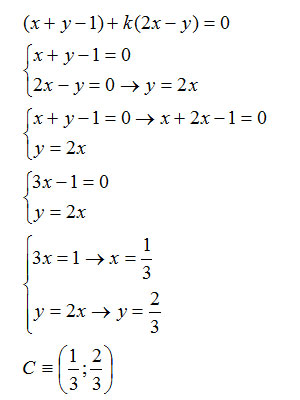
Esercizi da svolgere
Per assicurarvi di aver capito cosa sono i fasci di rette e come si svolgono gli esercizi, ecco qualche problema con cui potete esercitarvi. Restiamo come sempre a vostra disposizione attraverso il modulo contatti, per domande, informazioni o suggerimenti.
- Determina la retta del fascio improprio y=3x+q passante per il punto P(+1;-4)
- Nel fascio y=-2x+q determina a retta r che dista 4raq5 dal punto P(-2;+1)
Suggerimento: ricordati come si calcola la distanza di un punto da una retta - Determina il centro del fascio proprio di rette di equazione:
(3k-1)x+2ky-k+5=0
Suggerimento: cerca di “manipolare” l’equazione che ti è stata fornita in modo da ottenere quella principale del fascio proprio con le due rette generatrici. Intersecale ed avrai il centro. - Scrivi l’equazione del fascio proprio di centro C(2;4)