Coefficiente angolare di una retta – come si calcola? Formule ed esercizi

Il coefficiente angolare si indica in genere con la lettera m ed esprime la pendenza della retta, ovvero la sua inclinazione rispetto all’asse delle ascisse.

Il coefficiente angolare, in geometria analitica, lo si ritrova nell’equazione della retta y=mx+q e si calcola in vari modi. In questa lezione vedremo in maniera semplice (ma completa) tutto quello che c’è da sapere sui coefficienti angolari: dalla relazione con l’angolo dell’inclinazione della retta alle formule per calcolarlo.

Che cos’è il coefficiente angolare?

Definizione: il coefficiente angolare di una retta indica la pendenza di quest’ultima.

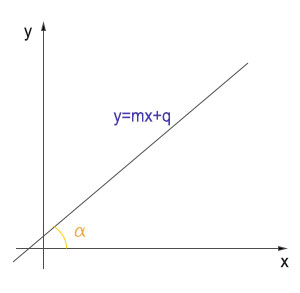
Ti ricordi l’equazione e la definizione di retta? Il coefficiente angolare è quel numero (compreso di segno) che trovi davanti la x. Facciamo un esempio:

y=-2x+3

Il coefficiente angolare è -2. Da notare che abbiamo incluso il segno meno e non la x, che è invece la variabile dell’equazione della retta.

NOTA: se davanti la x non vedi numeri, vuol dire che è sottinteso 1.

Come si calcola il coefficiente angolare?

Con la retta in forma esplicita

In questo caso hai l’equazione nella forma y=mx+q. Il calcolo del coefficiente angolare è estremamente semplice, visto che ti basta prendere il segno e il numero che trovi prima della x. Esattamente come nell’esempio precedente.

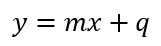
Con la retta in forma implicita

In questo caso l’equazione è nella forma ax+by+c=0. La tecnica di calcolo più semplice ed immediata è di trasformare l’equazione nella forma esplicita e seguire la regola vista prima.

Se vuoi una formula diretta, puoi utilizzare:

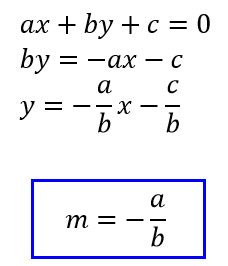
Ovviamente il termine b deve essere diverso da 0 altrimenti ci ritroviamo di fronte ad un’equazione differente e che rappresenta invece una retta verticale (ax+c=0)

Coefficiente angolare e pendenza della retta

Abbiamo detto che il coefficiente m di una retta è strettamente legato alla sua pendenza. Che relazione c’è però con l’angolo che si forma con l’asse delle ascisse?

In realtà il coefficiente angolare non rappresenta l’angolo, bensì la sua tangente. Cioè, in riferimento alla figura vista sopra:

m= tg α

Quindi possiamo dire brevemente che il coefficiente angolare è la tangente dell’angolo α.

Proprietà e valori noti

• Il coefficiente angolare è negativo se la retta è una funzione decrescente, cioè se è inclinata verso il basso.
• E’ nullo se si tratta di una retta orizzontale.
• Se la retta è verticale, il valore m non esiste. Per chi ha studiato analisi si può dire che m=∞.
• La bisettrice del primo e terzo quadrante ha m=1.
• La bisettrice del secondo e quarto quadrante ha m=-1.

Coefficiente angolare di rette parallele e perpendicolari

Visto che le rette parallele hanno stessa inclinazione, allora hanno anche lo stesso coefficiente angolare. Le rette perpendicolari sono ruotate di 90° l’una rispetto all’altra. Per questa ragione la m1=-1/m2.

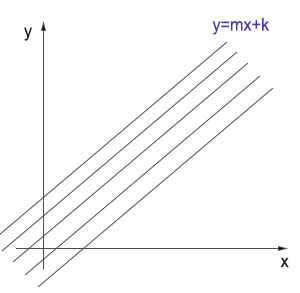
Il fascio improprio di rette è un’estensione del concetto di parallelismo. Visto che il fascio è formato interamente da rette parallele, allora l’equazione del fascio avrà un unico valore di m. Ciò che varia è invece l’intercetta all’origine.

Coefficiente angolare retta per 2 punti

Nel caso in cui la traccia ci fornisca le coordinate di due punti A e B, è possibile individuare il coefficiente della retta che passa per A e per B.

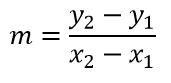
Esercizi con il calcolo coefficiente angolare

Esercizio 1

Determinare il coefficiente angolare della retta di equazione -2x+5y+3=0

Svolgimento

Come detto in precedenza, per evitare di imparare altre formule a memoria, conviene trasformare l’equazione della retta da implicita e esplicita. Per cui:

-2x+5y+3=0 → 5y=2x-3

y= 2/5 x – 3

m= 2/5

Esercizio 2

Calcolare il coefficiente angolare della retta passante per A(2;5) e B(-3;0).

Svolgimento

In questo caso o utilizziamo la formula vista in precedenza, o quella generica di retta per due punti.

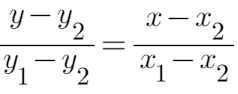
Andiamo a sostituire i dati che ci ha fornito la traccia.

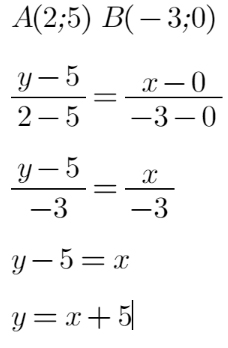
Approfondimenti: scopri gli esercizi sulla retta nel piano cartesiano

Conclusioni

In questa lezione abbiamo visto in maniera approfondita che cos’è e come si calcola il coefficiente angolare e la pendenza di una retta. Se gli appunti che abbiamo messo a disposizione ti sono stati utili, lascia un commento positivo. 

Ci aiuteranno a crescere a fornirti ogni giorno contenuti di qualità per tutti gli studenti italiani. Se hai dei dubbi o dei chiarimenti, il nostro staff è a tua disposizione.