Rette parallele e perpendicolari sul piano cartesiano

Continuiamo la trattazione della retta andando a definire cosa sono, come studiare e quindi le formule delle rette parallele e perpendicolari sul piano cartesiano.

Gli argomenti della lezione

Definizione di rette parallele

Definizione di rette perpendicolari

Formula delle rette parallele e perpendicolari

Qualche esempio per iniziare

Esercizi svolti

Dopo aver parlato dell’equazione della retta nella scorsa lezione, oggi parleremo di rette parallele e perpendicolari; formule e definizioni non saranno più un mistero e riusciremo a fine lezione a trattare un argomento che è più semplice di quello che si pensi.

[adrotate banner=”4″]

Definizione di rette parallele

Tralasciando le trattazione universitaria sui punti impropri, ci può essere sufficiente la definizione che viene data nelle scuole primarie:

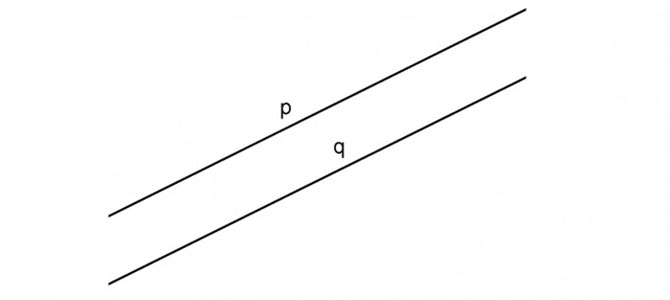
Per definizione due rette sono parallele quando non si intersecano mai

Definizione di rette parallele

Questo significa che due rette parallele possono essere semplicemente viste  come due retta traslate, cioè “spostate” senza aver subito alcuna rotazione.

Definizione di rette perpendicolari

Molto semplicemente possiamo dire che:

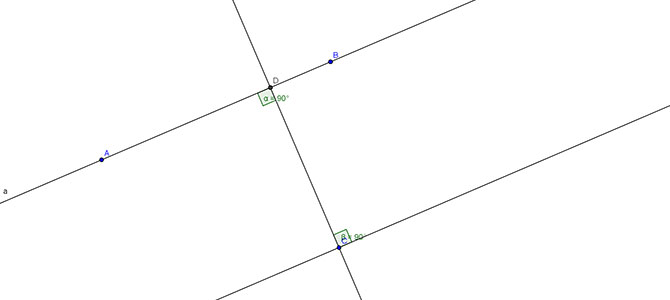
Per definizione due rette perpendicolari sono due rette  che, intersecandosi, formano 4 angoli retti.

Definizione di rette perpendicolari

Rette parallele e perpendicolari nel piano cartesiano

Ricordi l’equazione esplicita della retta y=mx+q ? Abbiamo detto che m si chiama coefficiente angolare e rappresenta l’inclinazione della retta. Non ci vuol molto ad osservare che due rette parallele per definizione hanno la stessa inclinazione. Per cui possiamo dire che:

Condizione di parallelismo nel piano cartesiano

Condizione necessaria e sufficiente affinché ci sia parallelismo è che le due rette abbiano lo stesso coefficiente angolare.

Nel caso in cui, invece, mi trovo di fronte a due rette parallele, la formula riguarda sempre il coefficiente angolare, ma questa volta devo scrivere:

Condizione necessaria e sufficiente affinché ci sia perpendicolarità è che i coefficienti angolari siano antireciproci tra loro.

Condizione di perpendicolarità nel piano cartesiano

Esempi di rette parallele e perpendicolari

y=3x+4 e y=3x+2 sono rette parallele in quanto il coefficiente angolare m è lo stesso, cioè pari a 3.

y=3x+3 e y=-1/3 x+3 sono rette perpendicolari in quanto il coefficienti angolare del secondo è l’antireciproco del primo.

Sostanzialmente, quando in un problema di geometria analitica, la traccia ci suggerisce la perpendicolarità o il parallelismo tra due rette, vuol dire che sta fornendo una fondamentale informazione sul coefficiente angolare.

Esercizi svolti

1. Trovare l’equazione della retta s parallela alla retta r:y=3x+2 e passante per l’origine.
   La retta che dobbiamo calcolare è s e, dato che non conosciamo nulla, partiamo dalla formula esplicita della retta, cioè s:y=mx+q. Le nostre incognite sono m e q.Poiché la traccia ci ha già detto che r ed s sono rette parallele nel piano cartesiano, allora hanno lo stesso coefficiente angolare, cioè m=3.
   Dobbiamo solo calcolare q. Ci serve quindi un altro dato. La traccia ci dice anche che passa per l’origine, cioè il punto O(0,0) appartiene alla retta. Per cui andando a sostituire il punto O nell’equazione della retta ho:
   y=mx+q
   0=m0+q
   q=0
   Poichè m=3 e q=0, allora ho trovato l’equazione della retta s:y=3x
2. Trovare l’equazione della retta t perpendicolare alla retta r:x+y-1=0 e passante per il punto Q(0;2)
   Anche in questo caso l’equazione della retta generica da cui partire è t:y=mx+q dove le nostre incognite sono m e q.Poiché ha evidenziato che t ed r sono rette perpendicolari nel piano cartesiano, vuol dire che il coefficiente angolare di t è l’antireciproco di r. Quanto vale il coefficiente angolare di r? Basta trasformare la formula della retta da implicita ad esplicita:
   x+y-1=0
   y=-x+1 –> m=-1
   Posso quindi calcolare il coefficiente angolare di t=-(-1/1)=+1
   Resta solo da calcolare il termine noto della retta (q). Ci serve un secondo dato oltre alla condizione di perpendicolarità. Dato che ci viene fornito come sempre dalla traccia, dato che la retta t passa per il punto Q. Questo vuol dire che posso sostituire le coordinate di Q nell’equazione della retta generica.
   t:y=mx+q
   2=m0+q
   q=2
   Trovati m e q, ho così risolto il problema e l’equazione della retta è: t:y=1x+2 che posso anche scrivere come t:y=x+2
   Puoi provare, in alternativa, a risolvere l’esercizio diversamente usando la formula della retta passante per un punto che troverai nelle prossime lezioni.