Il teorema della corda esprime la relazione tra la generica corda della circonferenza, il suo diametro e il seno di quello che viene definito angolo al centro.
In questa lezione vedremo qual è il teorema della corda, analizzandone enunciato, dimostrazione, formule (e formule inverse) ed alcuni interessanti esercizi svolti per mettere in pratica quanto appreso. Iniziamo subito ad enunciare questo importante teorema della trigonometria.
Enunciato
Teorema della corda – In una circonferenza una corda è uguale al prodotto del diametro per il seno dell’angolo alla circonferenza (acuto o ottuso) che insiste su essa.
Detta AB la corda, r il raggio della circonferenza e α l’angolo al centro, allora vale la relazione:
![]()
Dimostrazione del teorema della corda
Consideriamo una corda AB di una circonferenza di raggio r e un angolo qualsiasi ACB=α che insiste sulla corda AB ed inscritto ad esempio nell’arco maggiore BA, così come nella figura seguente.
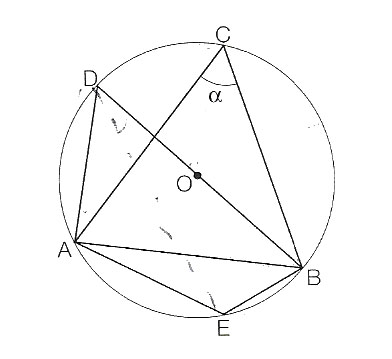
Sia BD il diametro della circonferenza passante per un estremo della corda. Poiché il triangolo ABD è rettangolo in quanto inscritto in una semicirconferenza valgono i teoremi della trigonometria sui triangoli rettangoli. Possiamo quindi scrivere che un cateto è uguale all’ipotenusa per il seno dell’angolo opposto.
Considerando il triangolo ABD, con angolo retto nel vertice A e bisettrice pari proprio all’ipotenusa BD, allora possiamo scrivere:
![]()
Poiché BD è il diametro allora possiamo scrivere:
![]()
Ma l’angolo ADB è uguale all’angolo ACB perché inscritti nello stesso arco AB, quindi:
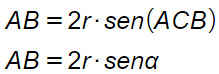
In questo modo abbiamo ottenuto la dimostrazione del teorema della corda in due semplici passaggi.
OSSERVAZIONE: Il teorema della orda vale anche se la corda AB coincide con il diametro. Infatti in tal caso α=90°, per cui il senα=1 ed AB=2rsenα diventa AB=2r.
Formule inverse
Dai teoremi sulle corde si possono ricavare 2 formule inverse che permettono di calcolare il raggio o il diametro di una circonferenza e l’angolo al centro.
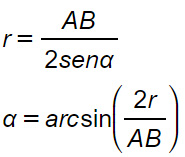
Da notare che, nella seconda formula inversa, è necessario applicare l’arcoseno per trovare la misura dell’angolo.
A cosa serve il teorema della corda
Il teorema della corda si rivela utile ogni volta che ci sono figure inscritte in una circonferenza. Ciò si verifica non solo nei problemi di trigonometria, ma anche in analisi e capita spesso anche negli esercizi della seconda prova di matematica durante gli esami di maturità.
Esercizi svolti
Esercizio 1
Determiniamo la lunghezza della corda AB di una circonferenza di raggio r, sottesa da un angolo α, tale che α=π/4.
Applichiamo direttamente la formula del teorema della corda:
AB=2r · senα
Dobbiamo in questo primo esercizio semplicemente sostituire al seno di alfa il seno di 45.
AB=2r · sen(π/4)=2r(√2/2)= r√2
Esercizio 2
In una circonferenza di raggio r due corde AB=(4/3)r e BC=(4/5)r sono consecutive e il centro della circonferenza è interno all’angolo ABC. Determiniamo il perimetro e l’area del triangolo ABC.
Determiniamo il seno degli angoli del triangolo usando proprio il teorema della corda.
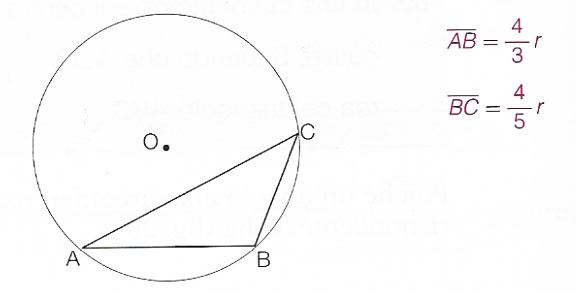
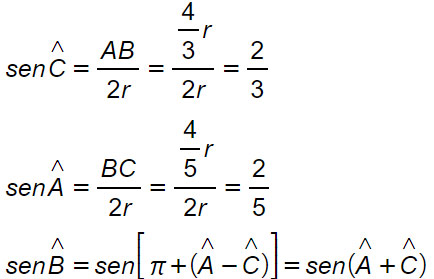
Una piccola considerazione merita l’angolo B. Lo abbiamo calcolato tenendo conto che B=180°-A-C. Per le formule sugli archi associati, il sin(180-α)=sen(α). Non conoscendo il valore dei due angoli, è necessario ricorrere alle formule di addizione. Per cui possiamo scrivere:
sen(A+C)=senA·cosC+cosA·senC
Dove il coseno di A e di C lo ricaviamo dall’equazione fondamentale della goniometria sen²a=1-cos²a. Per cui cosC=√5/3, cosA=√21/5. Per cui il coseno di B è pari a:
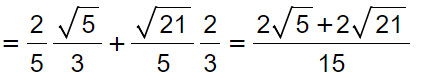
Possiamo così determinare il lato AC con il teorema della corda:
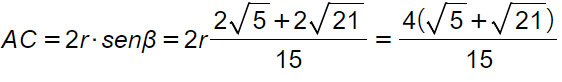
Possiamo così calcolare il perimetro e l’area.
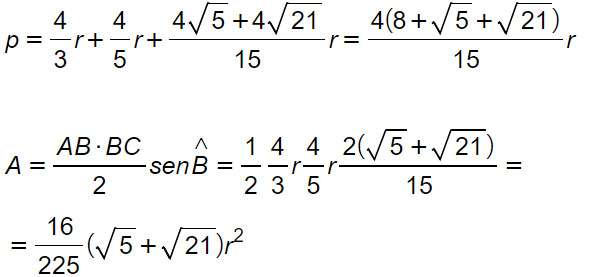
Conclusioni
Come hai potuto notare soprattutto in quest’ultimo esercizio, il teorema della corda riveste un ruolo importantissimo nei problemi in cui c’è un triangolo inscritto in una circonferenza. Per questa ragione, ti consigliamo almeno di memorizzare la formula e di tenerla pronta nel caso in cui dovesse servirti.