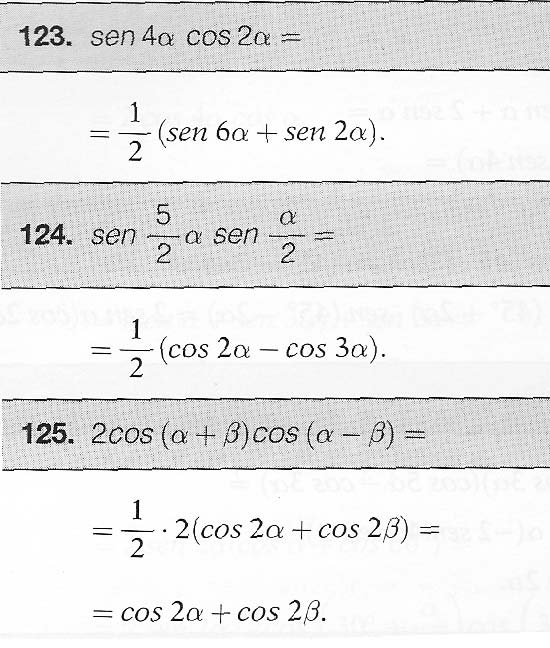Le formule di Werner permettono di trasformare il prodotto di due seni o di due coseni o di un seno per un coseno nella somma o differenza di seni e coseni. Completano il capitolo delle formule goniometriche e sono quelle meno utilizzate nelle equazioni perché portano ad uno sviluppo più complesso. Ecco la tabella completa:
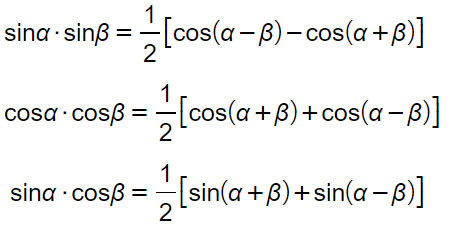
Vediamo subito concretamente 2 esempi per applicare le formule di Werner.
Esercizio 1
Calcoliamo (sin 37° 30′) · (cos 7° 30′)
Osserviamo che nel sistema di misura degli angoli (sessagesimale)
- la somma 37°30’+7°30′ = 45°
- la differenza 37°30′-7°30′ = 30°
Per cui possiamo scrivere che:
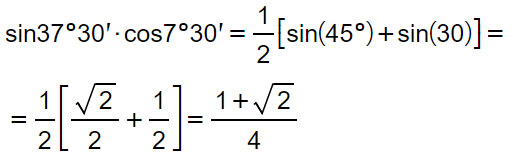
Esercizio 2
Trasformiamo in una somma il prodotto cos3x·cos5x
Abbiamo:
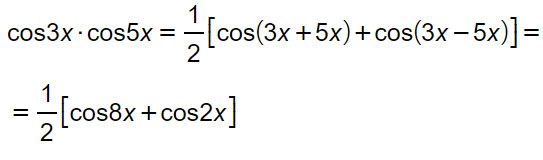
Dimostrazione
Le formule di Werner si ottengono direttamente dalle formule di Prostaferesi. In alternativa possono essere ricavate anche della formule di addizione e sottrazione.
Prima formula di Werner
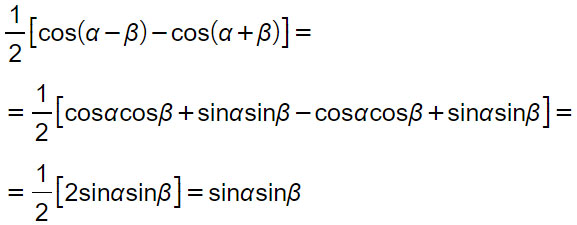
Seconda formula di Werner
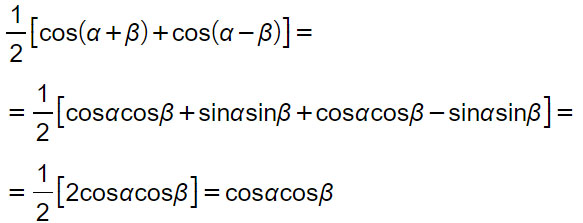
Terza formula di Werner
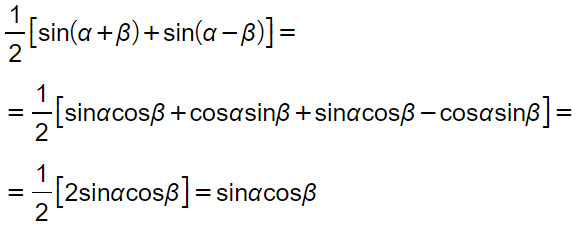
Curiosità
Le formule di Werner devono il loro nome allo scienziato che le ideò nel XVI secolo. Nonostante non vengano oggi molto utilizzate, hanno portato alle formule di Prostaferesi, all’epoca molto utili ai naviganti per il tracciamento delle rotte in mare.
Esercizi risolti
Trasformiamo in prodotti le seguenti somme con le formule di Werner.