Che cos’è il circocentro di un triangolo? Che differenze ci sono tra il circocentro di un triangolo rettangolo e tutti gli altri tipi di triangoli? Esistono delle formule anche in geometria analitica che ci permettano di calcolarlo? Grazie, Emanuele.
Un nostro studente ci ha chiesto una lezione di approfondimento sul circocentro del triangolo. Per prima cosa diamo subito una definizione:
Il circocentro è il punto di intersezione degli assi di un generico triangolo. Si dimostra anche che è il centro della circonferenza circoscritta al medesimo triangolo.
Questo significa che, disegnando gli assi dai vertici di un qualsiasi triangolo, questi si intersecano in un punto chiamato circocentro. Ti ricordi cosa sono gli assi di un triangolo? Sono i segmenti perpendicolari ad ogni lato e passanti per il suo punto medio. Proviamo a disegnarli e a vedere cosa succede…
Circocentro del triangolo scaleno acutangolo
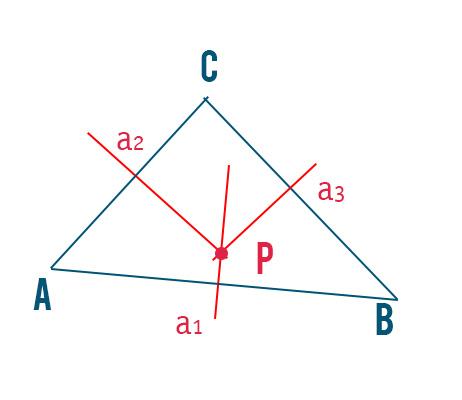
Dato il triangolo scaleno ABC, disegnamo per ogni lato il rispettivo asse. Per cui possiamo individuare l’asse a1 sul lato AB, l’asse a2 sul lato AC e l’asse a3 sul lato BC. Intersecando i tre assi otteniamo il circocentro del triangolo, indicato in figura con il punto P.
Circocentro del triangolo scaleno ottusangolo
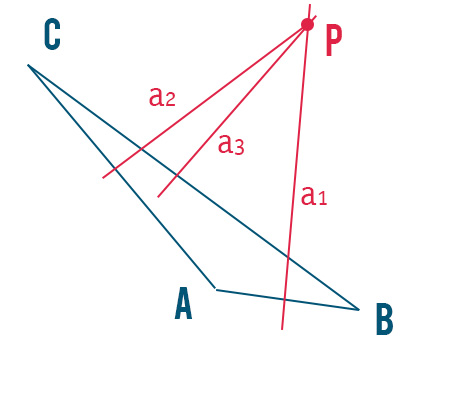
Dato il triangolo ottusangolo avente l’angolo maggiore di 90° nel vertice A. Abbiamo disegnato i tre assi a1, a2, a3. Cosa si nota? Che il punto trovato questa volta è esterno. Possiamo quindi dedurre la seguente regola valida per il circocentro:
- nel triangolo acutangolo è interno alla figura;
- nel triangolo ottusangolo è esterno alla figura;
Vediamo ora alcuni casi di triangoli particolari.
Circocentro del triangolo rettangolo
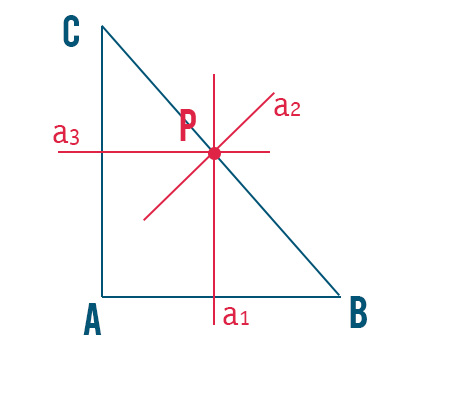
Dato il triangolo rettangolo ABC retto nel vertice A. Abbiamo disegnato per ogni lato i rispettivi assi e quello che si nota è che il circocentro di un triangolo rettangolo non è altro che il punto medio dell’ipotenusa.
Circocentro del triangolo isoscele
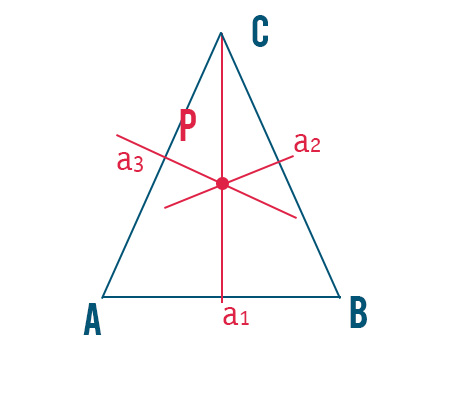
Il circocentro del triangolo isoscele gode di un’interessante proprietà. Se provassimo a disegnare baricentro, incentro e ortocentro di un triangolo isoscele ci accorgeremmo che questi sono allineati ed appartengono proprio all’altezza.
Circocentro del triangolo equilatero
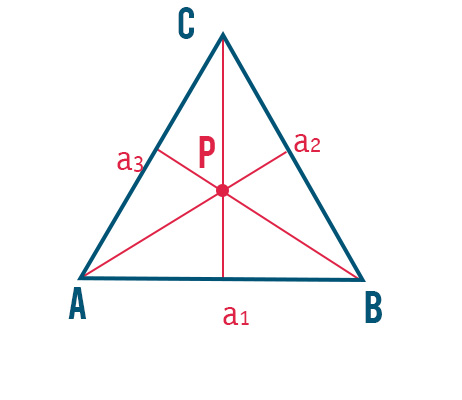
PROPRIETA’: dato il triangolo equilatero ABC, incentro, baricentro e ortocentro sono tra loro coincidenti.
Circocentro in geometria analitica
Come si fa a determinare il circocentro di un triangolo avendo a disposizione, ad esempio, solo i 3 vertici del triangolo stesso? Un primo metodo, più rapido e che consigliamo di applicare è quello di sfruttare la definizione di circocentro: è la circonferenza circoscritta al triangolo. Questo vuol dire che è equidistante dai 3 vertici del triangolo. Dato quindi il triangolo ABC, considerando H il circocentro, bisognerà imporre che:
AH=BH=CH
dove H viene tenuto come incognita H(xH, yH).
Un secondo metodo, più lungo e che richiede più passaggi anche a livello meccanico, prevede l’applicazione di una costruzione particolare. I passi a fare sono i seguenti:
- calcoliamo la formula della retta dei tre lati del triangolo;
- calcoliamo le coordinate del punto medio di ogni lato;
- calcoliamo l’asse per ogni lato applicando la formula della retta passante per un punto e coefficiente angolare noto (se m è il coefficiente della retta passante per il lato, noi prenderemo -1/m rispettando la condizione di perpendicolarità)
- intersechiamo tra loro due rette per ottenere il punto H cercato.
Esercizio
Determinare il circocentro del triangolo avente vertice nei punti A(7;1) B(2;7) e C(-2:-2).
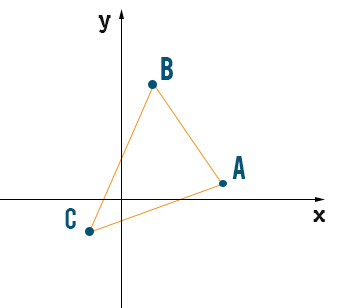
Come detto in precedenza applichiamo la definizione vista ad inizio lezione, cioè che il circocentro è il centro della circonferenza circoscritta al triangolo. Per cui H è equidistante da A, B e C.
AH=BH=CH
Si tratta quindi di analizzare 2 equazioni in 2 incognite (ascissa e ordinata del punto H).
AH=BH
BH=CH
Volendo di potrebbe usare anche l’equazione AH=CH ma, poiché le incognite sono 2, possiamo servirci di 2 equazioni e trascurarne una terza.
AH=BH lo imponiamo andando a calcolare la distanza tra due punti tenendo H come incognita.
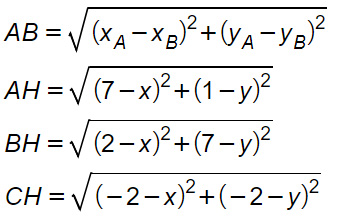
A questo punto non ci resta che imporre le uguaglianze AH=BH e BH=CH.
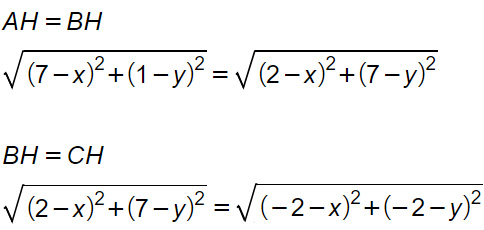
A questo punto non ci resta che risolvere parallelamente queste due che possiamo inserire in un sistema di equazioni.

Abbiamo così alla fine calcolato il circocentro del triangolo individuandone le coordinate x e y.
Conclusioni
Abbiamo visto in questa lezione tutto quello che c’è da sapere sul circocentro, analizzandone proprietà e caratteristiche in funzione anche al tipo di triangolo. Nell’esempio svolto, da applicare al programma di geometria analitica per gli studenti delle scuole superiori, abbiamo semplicemente applicato la definizione di questo punto caratteristico dei triangoli per trovare più o meno rapidamente le soluzioni del problema.
Se questa lezione ti è stata utile o se hai ancora dubbi o perplessità, lascia un commento qui in basso. Il nostro staff ti risponderà nel minor tempo possibile.