Nella lezione di oggi vedremo cosa sono i sistemi di equazioni di primo grado. Spiegazione, esercizi svolti per imparare a risolvere i sistemi di primo grado a due incognite, all’inizio, per complicare poi ed arrivare a capire come risolvere i sistemi a tre incognite.
Gli argomenti della lezione
- Introduzione
- Definizione di sistema di equazioni?
- Metodo di sostituzione
- Metodo del confronto
- Metodo dell’addizione e sottrazione
- Metodo di Cramer
- Quale metodo scegliere per risolvere i sistemi?
Introduzione alla lezione
Nelle precedenti lezioni abbiamo analizzato le regole per risolvere le equazioni di primo grado, risolvendo esercizi svolti con un crescente grado di difficoltà anche sulle equazioni fratte.
Ma in tutti gli esercizi sulle equazioni di primo grado visti fino a questo momento, abbiamo incontrato un’unica incognita, ovvero la x. Come risolvere le equazioni con più incognite?
Cosa sono i sistemi di equazioni?
La regola generale vuole che:
Il numero di equazioni deve essere pari al numero di incognite affinché gli esercizi siano risolvibili.
Senza entrare troppo in dettagli tecnici non di competenza di queste lezioni di matematica, ci basti dire che se abbiamo 2 incognite, abbiamo bisogno di risolvere 2 equazioni. Se le incognite sono 3 dovremo risolvere 3 equazioni e così via…
Per risolvere più equazioni contemporaneamente abbiamo bisogno dei sistemi di equazioni.
I sistemi di equazioni servono quindi a calcolare più incognite da più equazioni, appunto, messe a sistema, cioè graficamente unite in colonna all’interno di una parentesi graffa.
Metodi per risolvere i sistemi di equazioni
La lezione di oggi è particolarmente importante perché i metodi che stiamo per vedere sono validi non solo per i sistemi di equazioni di primo grado, ma anche di grado superiore al primo. Useremo cioè le stesse tecniche risolutive anche per risolvere gli esercizi sui sistemi di secondo grado, terzo grado, eccetera.
Si tratta del metodo più utilizzato e che può andare bene per tutti i tipi di sistemi di equazioni. Si tratta di un metodo semplice, ma che spesso comporta dei calcoli in più.
Durante una verifica o un compito in classe, quando si è sotto pressione e il tempo scarseggia, capita spesso agli studenti di commettere errori banali di calcolo: basta un segno dimenticato e l’esercizio non si trova più. Attenzione quindi a svolgere sempre i calcoli con la massima concentrazione.
Per capire come risolvere i sistemi di equazioni di primo grado con il metodo della sostituzione, proviamo assieme ad affrontare un esercizio svolto.
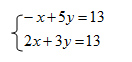
Vediamo che in entrambe le equazioni del sistema ci sono tutte le incognite, sia la x che la y. Iniziamo a risolvere il sistema di primo grado partendo dall’equazione che ci sembra più semplice e calcolandoci l’incognita col coefficiente più semplice. Nel nostro caso tra le due equazioni noto che alla prima x praticamente non c’è un coefficiente – cioè è sottinteso 1. Quindi inizio a scrivere:
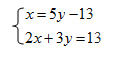
A questo punto sostituisco, da cui il nome metodo di sostituzione dei sistemi, la x che ho calcolato nella seconda equazione:
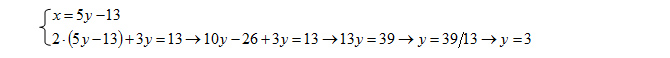
Una volta calcolato il valore della seconda incognita, cioè y=3, sostituisco nuovamente questo risultato nella prima equazione, cioè torno al primo rigo:
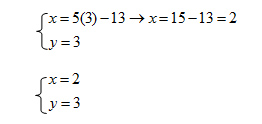
La domanda che giustamente potrebbe porsi lo studente più attento sarebbe: “Cosa sarebbe accaduto se avessi calcolato la y nel primo passaggio invece della x?”
Il risultato del sistema di primo grado non sarebbe cambiato ma avrei soltanto complicato leggermente i calcoli. Per convincertene, eccone la dimostrazione: risolviamo lo stesso esercizio, calcolando stavolta la y.
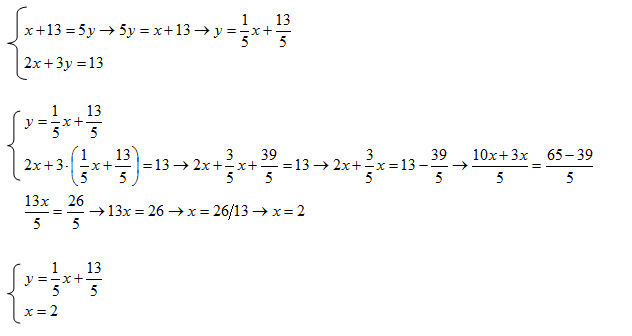
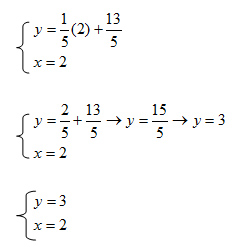
I sistemi di equazioni di primo grado sono più raramente risolti con il metodo del confronto. Il metodo, non molto difficile in realtà, consiste nel calcola la stessa incognita in entrambe le equazioni e poi sfruttare la proprietà: se A=B e A=C allora B=C. Vediamo subito lo stesso esercizio di prima risolto stavolta con il metodo del confronto dei sistemi lineari:
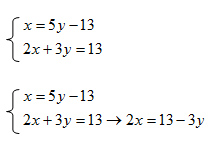
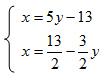
A questo punto, avendo calcolato la x in entrambe le equazioni, posso eguagliare i secondi membri, scrivendo:
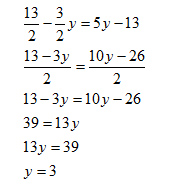
Avendo calcolato la seconda incognita, sostituisco il risultato in una delle due equazioni di partenza – è indifferente quale – per risolvere il sistema e ottenere anche la prima incognita.
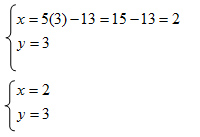
Si tratta a nostro avviso di uno dei metodi più semplici da utilizzare per risolvere i sistemi di equazioni. Certamente è tra i più rapidi dato che in presenza di due equazioni lineari consente di individuare abbastanza rapidamente la soluzione del sistema. Il medoto dell’addizione e sottrazione consiste semplicemente nell’addizionare e sottrarre le equazioni che compongono il sistema.
Il trucco per risolvere i sistemi a due incognite con il metodo dell’addizione e sottrazione è di fare in modo che i coefficienti di almeno un’incognita siano uguali.
Vediamo sempre l’esercizio precedente:
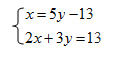
Innanzitutto facciamo in modo che tutte le incognite siano a sinistra e i termini noti a destra.
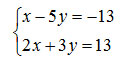
Vado ora a guardare i coefficienti delle incognite, cioè i numeri delle x e delle y. Devo fare in modo che nelle due equazioni, i coefficienti di almeno un’incognita siano uguali. Ciò significa che dobbiamo trasformare l’equazione usando la proprietà della moltiplicazione e della divisione.
Se provo infatti a moltiplicare per 2 la prima equazione, primo e secondo membro, ottengo:
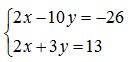
A questo punto tutte le incognite x hanno lo stesso coefficiente, cioè 2.
La regola generale è che tra i coefficienti dell’incognita delle due equazioni va calcolato il minimo comune multiplo. Successivamente si esegue la divisione tra mcm e il coefficiente dell’incognita: quello sarà il numero per cui moltiplicare l’intera equazione.
Vediamo se, ad esempio, se vogliamo ridurre allo stesso coefficiente le y anziché le x.
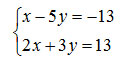
Calcolo il mcm tra 5 e 3, pari cioè a 15. Dato che 15:5=3, vuol dire che la prima equazione va moltiplicata tutta per 3. Poiché invece 15:3=5, vuol dire che la seconda equazione dovrò moltiplicarla tutta per 5. Ottengo così:
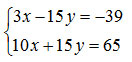
Ho così capito come uguagliare i coefficienti delle equazioni. E’ facile rendersi conto che il primo caso è stato decisamente più semplice dato che uno dei coefficienti era 1.
Ora basta vedere il segno dei due coefficienti uguali calcolati.
- se sono uguali, si esegue la sottrazione tra le equazioni
- se sono opposti, si esegue l’addizione tra le equazioni
Poiché -15y e +15y sono numeri relativi opposti, si calcola l’addizione tra le equazioni, cioè si sommano le x, si sommano le y e si sommano i termini noti.
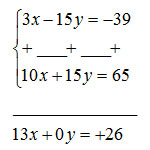
E’ importante notare che uno dei coefficienti dell’equazione risultante è pari a 0, se ciò non dovesse accadere vuol dire che abbiamo sbagliato qualche calcolo e dobbiamo rifare da capo.
A questo punto ho ottenuto un’unica equazione di primo grado: 13x=26 il cui risultato è semplicemente x=2.
Individuata la prima incognita, la sostituisco in una delle due equazioni, per semplificare i calcoli, è opportuno scegliere l’equazione più semplice.
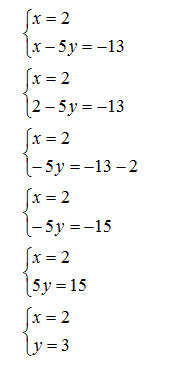
Ho così trovato lo stesso risultato individuato nei metodi precedenti, ma forse in maniera più semplice.
Metodo di Cramer
Il metodo di Cramer è l’ultimo dei metodi analizzati. Viene molto utilizzato nei sistemi più semplici, dato che si tratta di svolgere semplici calcoli numerici. Tuttavia diventa abbastanza laborioso quando i sistemi di equazioni andranno complicandosi.
Partiamo come sempre dall’esercizio precedente:
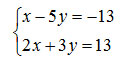
Per risolvere il sistema di primo grado con il metodo di Cramer è necessario calcolare 3 numeri, chiamati determinanti ed indicati con la lettera greca Delta.
Come calcolare il determinante del metodo di Cramer?
Il determinante del metodo di Cramer è un insieme di 4 numeri disposti su due righe e due colonne di una piccola tabella.
Il determinante si calcola facendo il prodotto del numero in alto a sinistra per quello in basso a destra. Da esso si sottrae il prodotto del numero in basso a sinistra per quello in alto a destra.
Il primo passo è costruire tre piccole tabelle di numeri, chiamate matrici, partendo dai coefficienti dell’equazione lineare. Per individuarle inizio 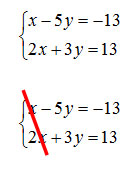
Per risolvere con il metodo di Cramer, dal sistema di primo grado immagino di eliminare tutti i termini con la x e considero tutti i coefficienti, cioè i numeri, che restano e li sistemo su una piccola tabella, detta matrice, nello stesso ordine:
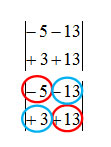
Moltiplico i termini sulla prima diagonale, in rosso, metto un segno meno e moltiplico i termini sulla seconda diagonale, in blu. Dato che ho eliminato i termini con la x, sto calcolando il DELTA X.
Δx=(-5)(+13)-(-13)(+3)=-65+39=26
Calcolo ora DELTA Y, immaginando di eliminare la y, dal sistema.
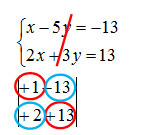
Δy=((+1)(+13)-(-13)(+2)=+13+26=+39
Infine si calcola l’ultimo determinante, immaginando di eliminare tutti i termini noti. Avrò così calcolato DELTA.
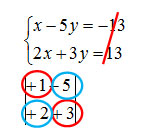
Δ=(+1)(+3)-(-5)(+2)=+3+10=+13
A questo punto non mi resta che fare tre semplici calcoli:
x=Δx/Δ=26/13=2
y=Δy/Δ=39/13=3
Ho imparato, così, anche a risolvere i sistemi di equazioni con il metodo di Cramer.
Quale metodo usare per risolvere i sistemi di primo grado?
Si tratta di una domanda più che legittima, dato che tutti i metodi di risoluzione dei sistemi portano alla stessa equazione. Tuttavia occorre tener conto che nei sistemi di secondo grado, si utilizzerà prevalentemente il metodo della sostituzione, per cui è bene conoscerlo bene.
Il metodo di Cramer è probabilmente quello su cui gli insegnanti insistono di più. Dal nostro punto di vista, il più semplice resta il metodo della somma e della differenza, fermo restando che tutti portano alla soluzione esatta.
Ora non ti resta che iniziare a risolvere da solo un po’ di esercizi sui sistemi di equazioni di primo grado. Ovviamente per dubbi, chiarimenti o segnalazioni restiamo a tua completa disposizione: contattaci.
Buon lavoro!
Complimenti Definizione molto accurata ed efficiente , sui calcoli e sugli step.