Equazione della retta passante per un punto: è una formula che permette di calcolare l’equazione di una retta nel piano cartesiano noto il coefficiente angolare ad un punto generico P. In questa lezione vedremo qual è la formula e come applicarla con degli esempi svolti e commentati.
Abbiamo già visto come calcolare l’equazione della rette per due punti. In questo caso dobbiamo fare una piccola differenza. Mentre prima i due dati a disposizione erano le coordinate di due generici punti, ora abbiamo bisogno sempre di due dati, ma uno dei due è il coefficiente angolare della retta. Vedrai che la formula è anche più semplice della precedente e ti permette di calcolare la retta per un punto in pochi passaggi.
Retta passante per un punto e coefficiente angolare noto
L’equazione della retta per un punto si può calcolare con la formula:
![]()
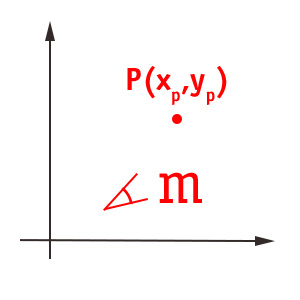
Dove xp e yp sono le coordinate del punto generico P, m è il coefficiente angolare della retta.
Come si arriva alla formula?
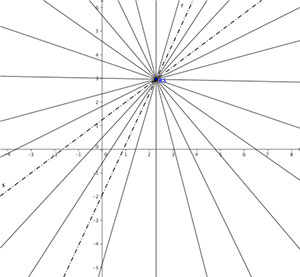
Retta Passante per un punto – Fascio proprio
Immaginiamo di voler disegnare una retta passante per un punto P, siamo davvero sicuri di poter a disegnare una sola retta? Dato che non ne conosciamo l’inclinazione, vuol dire che potremmo disegnare infinite rette per il punto, ottenendo quello che in geometria viene chiamato fascio proprio di rette.
Questo in geometria significa che l’appartenenza della retta al punto non è un dato sufficiente per trovare l’equazione della retta. Abbiamo cioè bisogno di un ulteriore dato.
Cerchiamo di capire bene un aspetto della retta: y=mx+q. Nella formula della retta le incognite sono due, m e q, per cui avremo bisogno di due dati. Il primo è l’appartenenza del punto P alla retta e il secondo?
Esempi sull’equazione della retta per passante per un punto
Esercizio 1
Calcolare l’equazione della retta passante per un punto P(4,1) e di coefficiente angolare m=3.

L’esercizio, risolvibile in pochi semplici passaggi, è stato svolto sostituendo le coordinate del punto P nell’equazione generica della retta. Ricordandoci i calcoli letterali dell’algebra, abbiamo isolato al primo membro la y, per ottenere così l’equazione della retta esplicita.
Sarà molto difficile negli esercizi trovare il coefficiente angolare già espresso, è molto più probabile trovare dei casi in cui ci venga richiesto di calcolare la formula della retta passante per un punto e parallela ad una retta, oppure l’equazione della retta passante per un punto e perpendicolare ad una retta. Vediamo questi due casi direttamente con degli esercizi svolti.
Esercizio 2 – Retta passante per un punto e perpendicolare ad una retta
Scriviamo l’equazione passante per un punto e perpendicolare ad una retta. Il punto è P(1;-2) mentre la retta è s:3y+6x-1=0
I dati a disposizione sono due: la retta incognita r passa per il punto P ed è perpendicolare alla retta s. Da questo secondo dato possiamo ricavare immediatamente il coefficiente angolare. Dalla lezione sulle rette parallele e perpendicolari abbiamo infatti scoperto che la condizione di perpendicolarità implica che i coefficienti angolari siano antireciproci.
Quindi iniziamo calcolando il coefficiente angolare della retta perpendicolare s.

A questo punto sfrutto il secondo dato che mi viene dato dalla traccia, l’appartenenza di P ad r, usando la formula vista ad inizio lezione.
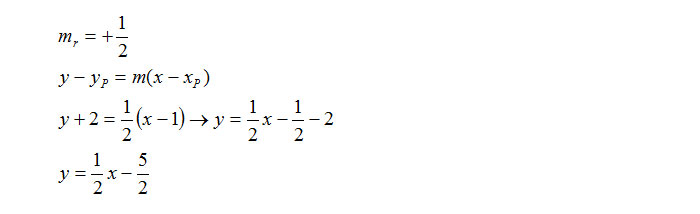
Esercizio 3 – Retta passante per un punto e parallela ad una retta
Scriviamo l’equazione della retta passante per un punto e parallela ad una retta dove il punto è P(2,3) e la retta è s:2x+y-7=0
L’esercizio è praticamente identico al precedente, anzi più semplice dato che i coefficienti angolari delle due retta parallele sono identici. Per cui possiamo proseguire spediti e risolvere agevolmente questo esercizio svolto:
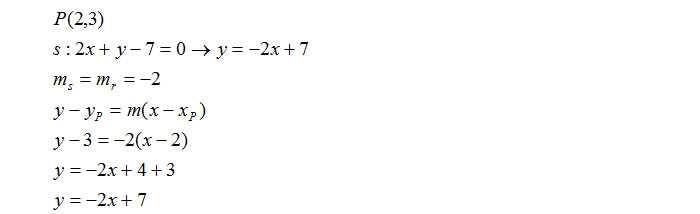
Esercizi da svolgere a casa
- Determina l’equazione della retta passante per P(-1;-4) e parallela alla retta di equazione y=2x-5
- Determina l’equazione della retta passante per P(+2;0) e perpendicolare alla retta di equazione 2x-3y+1=0
- Determina l’equazione della retta parallela alla retta di equazione 3x-2y=0 e passante per il punto di intersezione delle due rette x-y+3=0 e x+y+5=0.
(suggerimento: in questo caso non abbiamo il punto P, ma sappiamo che questi non è altro che l’intersezione tra le due rette, per cui basta risolvere il sistema tra le due equazioni delle rette…) - Determina il valore di a per il quale le due rette x-ay+3=0, (a+1)x+ay-3=0 non sono parallele.
Come faccio a trovarmi una retta passante per un punto senza sapere il coefficiente angolare della retta?
Non si può trovare una retta univocamente conoscendo un punto. Quello che tu puoi determinare è un fascio di rette (proprio). Infatti se ci pensi, se provi a fissare sugli assi cartesiani 1 punto, potrai disegnare infinite rette passante per quest’ultimo con inclinazione variabile.