Diagonale parallelogramma – come calcolarle? Quale formula usare?

Qual è la diagonale del parallelogramma? Quali sono le sue proprietà e come la si può calcolare? Esiste una formula specifica per determinare le diagonali del parallelogramma? Vi sarei molto grato se riusciste a farmi un esempio pratico sull’argomento. Grazie – Luca

Soluzione

La diagonale del parallelogramma è il segmento che unisce due vertici opposti. Ogni parallelogramma ha due diagonali e, come puoi vedere dalla figura sotto, con dimensioni differenti. Il parallelogramma ha una diagonale maggiore (d1) e una diagonale minore (d2).

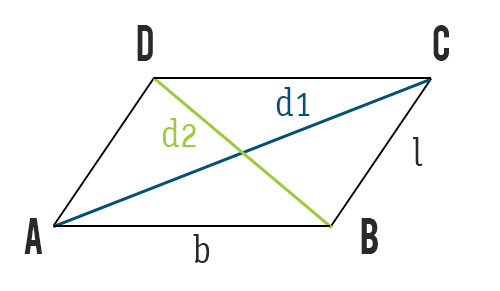
Formule diagonale parallelogramma

Come si possono calcolare le diagonali di un parallelogramma? Esiste una formula specifica? Esistono 2 formule, non molto conosciute e neanche molto utilizzate che tuttavia ti riportiamo.

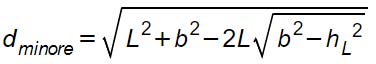
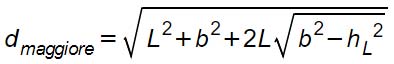
dove:

• d_minore e d_maggiore sono rispettivamente diagonale minore e diagonale maggiore;
• L è il lato obliquo
• b è la base
• h_L è l’altezza relativa al lato obliquo.

Come calcolare la diagonale del parallelogramma?

A seconda che sia la diagonale maggiore o minore puoi usare due formule diverse anche se molto simili tra loro. C’è solo un segno a fare la differenza. Avrai bisogno della misura della base, del lato obliquo e dell’altezza relativa al lato obliquo. Proprio quest’ultima è quella che mette più in difficoltà gli studenti perché non viene quasi mai data dalla traccia.

Per calcolarla puoi usare la formula inversa dell’area. Ti ricordi come si calcola l’area del parallelogramma noto il lato obliquo?

A=L×h_L → h_L =A/L

Ti basta quindi dividere l’area per il lato obliquo.

Da notare che nella formula per determinare la diagonale del parallelogramma c’è una radice di radice. Non farti troppi problemi, sostituisci i dati a disposizione e fai i calcoli senza badare alle radici quadrate.

Esempi

Per fissare meglio i contenuti, vediamo qualche problema risolto così da capire anche meglio come applicare le formule viste.

Esercizio 1

Determina le diagonali del parallelogramma ABCD in figura

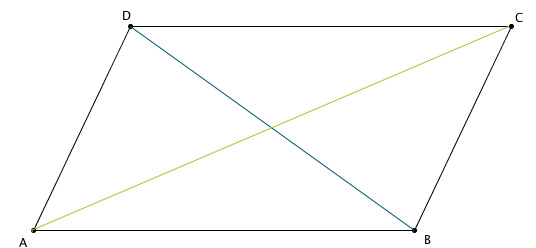
Dove

• AB=20 cm
• BC=10 cm
• A = 125 cm²

Per poter calcolare la diagonale di un parallelogramma, sia quella minore che quella maggiore, è necessario determinare prima l’altezza relativa al lato obliquo. Per cui sfruttiamo la formula inversa dell’area.

h_L =A/L = 125/20

h_L = 6,25 cm

A questo punto inseriamo tutti i dati nella formula della diagonale parallelogramma. Iniziamo da quella maggiore.

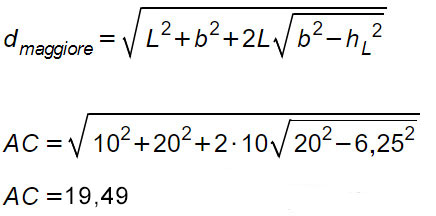
A questo punto completiamo l’esercizio calcolando anche la diagonale minore.

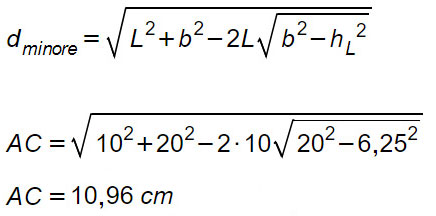
Conclusioni

In questa lezione abbiamo appreso come calcolare la diagonale di parallelogramma, sia quella minore che la maggiore. Si tratta di problemi che difficilmente si incontreranno nei vari esercizi da risolvere, ma vale la pena però segnarsi la formula, così da saperla usare se dovesse servire.

Se questa lezione ti è stata utile o hai ancora dubbi in materia, lascia un messaggio nei commenti sotto. Ci aiuterà a migliorare la qualità delle lezioni (che continueranno ad essere sempre gratis per i nostri lettori).