Andrea ci scrive una mail riportando i propri dubbi sull’argomento quadranti piano cartesiano: “Salve, avrei bisogno di un chiarimento in merito ai quadranti del piano cartesiano. Quali sono? Non riesco mai a ricordarli e faccio spesso confusione. C’è un modo per ricordarli? Volevo inoltre chiedervi se esiste un metodo per capire a quale quadrante appartiene un punto. Grazie – Andrea”
RISPOSTA
Quando ci si approccia al programma di geometria analitica, uno dei primi argomenti teorici trattati in classe è l’asse cartesiano e il sistema di ascissa e ordinata del generico punto. Una delle conseguenza di queste prime lezioni consiste nell’individuazione dei quadranti del piano cartesiano e seguono alcune riflessioni utili che ci semplificheranno la vita in molti casi.
Piano cartesiano quadranti – definizione
Vengono chiamati quadranti del piano cartesiano le quattro aree in cui resta diviso il piano dagli assi cartesiani.
Detto in parole povere l’asse delle ascisse (x) e quello delle ordinate (y) intersecandosi mi dividono lo spazio in 4 aree. Queste vengono chiamate quadranti cartesiani (o quadranti degli assi cartesiani). Vediamo subito con un disegno…
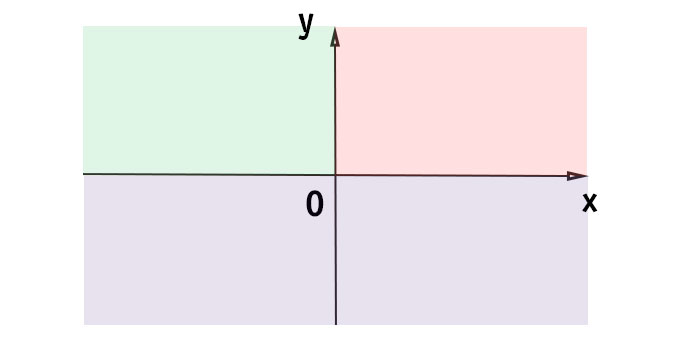
Quadranti piano cartesiano
Ordine quadranti piano cartesiano
Resta da rispondere ora alla domanda: quali sono i quadranti del piano cartesiano? Come fare per numerarli?
Primo quadrante
Convenzionalmente viene riconosciuto come primo quadrante l’area delimitata dagli assi positivi sia delle x che delle y.
IN PAROLE POVERE: il primo quadrante è quello in alto a destra
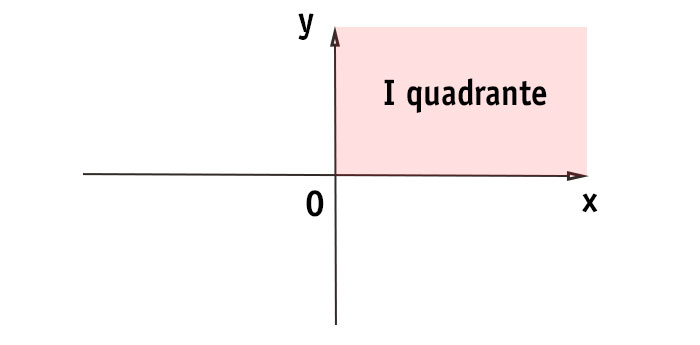
Primo quadrante
Segni primo quadrante (+;+)
Tutti i punti appartenenti al primo quadrante hanno sia l’ascissa che l’ordinata positiva. Quindi quando ti trovi di fronte un generico punto che ha sia la x che la y positiva, puoi stare sicuro che appartiene al primo quadrante.
Secondo quadrante
Convenzionalmente viene riconosciuto come secondo quadrante l’area delimitata dalla parte negativa dell’asse x e la parte positiva dell’asse y.
IN PAROLE POVERE: il secondo quadrante è quello in alto a sinistra
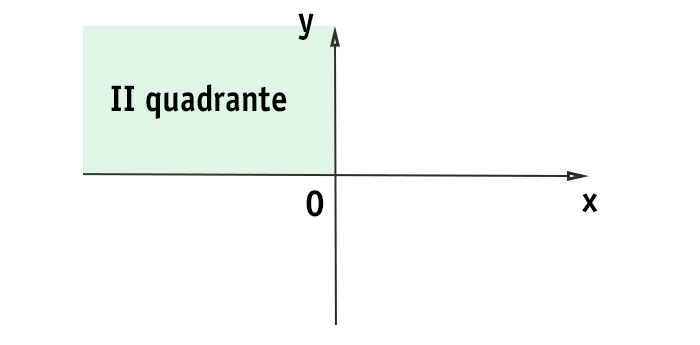
Secondo quadrante
Segni secondo quadrante (-;+)
Tutti i punti appartenenti al secondo quadrante hanno ascissa negativa e ordinata positiva. Per cui quando ti trovi di fronte ad un generico punto con x negativa e y positiva, puoi stare certo che appartiene al secondo quadrante.
Terzo quadrante
Convenzionalmente viene definito terzo quadrante, la regione del piano cartesiano che si forma dall’intersezione della parte negativa sia dell’asse delle x che delle y.
IN PAROLE POVERE: il terzo quadrante è quello in basso a sinistra
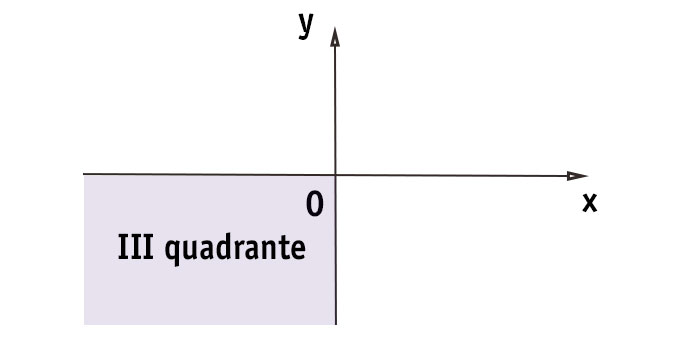
Terzo quadrante
Segni terzo quadrante (-;-)
Tutti i punti appartenenti al terzo quadrante hanno ascissa negativa e ordinata negativa. Per cui quando ti trovi di fronte ad un generico punto che ha entrambe le coordinate negative, puoi stare certo che appartiene al terzo quadrante.
Quarto quadrante
Convenzionalmente viene definito quarto quadrante, l’area del piano cartesiano che si forma dall’intersezione della parte positiva dell’asse delle x con quella negativa delle y.
IN PAROLE POVERE: il terzo quadrante è quello in basso a destra.
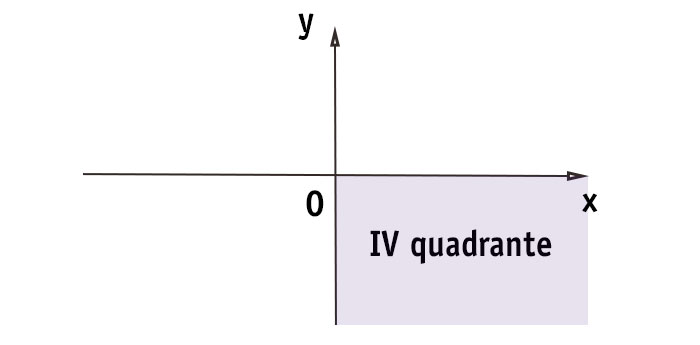
Quarto quadrante
Segni quarto quadrante (+;-)
Tutti i punti appartenenti al terzo quadrante hanno ascissa positiva e ordinata negativa. Per cui quando ti trovi di fronte ad un generico punto che ha x positiva e y negativa, puoi essere sicuro che appartiene all’ultimo dei quadranti del piano cartesiano.
Per non confondersi
REGOLA GENERALE: ti basta ricordare la posizione del primo quadrante e quella degli altri la ricavi di conseguenza. Infatti se il primo quadrante degli assi cartesiani è quello in alto a destra, gli altri li individui proseguendo in senso antiorario.
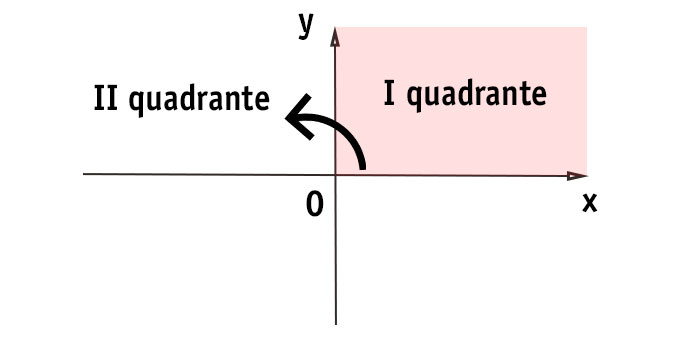
Come puoi vedere dalla figura, partendo dal primo quadrante procedi verso sinistra (rotazione antioraria come ti mostra la freccia) e individui il secondo quadrante. Procedendo ulteriormente nello stesso verso troverai quindi terzo e quarto quadrante.
Esercizi quadranti piano cartesiano
Se stai svolgendo il programma di matematica dedicato alla geometria analitica, hai probabilmente già studiato le equazioni e le disequazioni di primo grado e le equazioni e i sistemi di primo grado. Proviamo allora a risolvere insieme il seguente esercizio.
Sia dato il punto P(k-3;k+4). Stabilire per quali valori di k il punto P appartiene al primo quadrante
Ricordi cosa abbiamo detto prima? Che tutti i punti appartenenti al primo quadrante hanno ascissa negativa e ordinata positiva. Questo vuol dire che sia la x di P devono essere maggiori di zero. Quindi vuol dire che:
k+3>0
k+4>0
Le condizioni devono verificarsi contemporaneamente per cui possiamo risolvere come un sistema di disequazioni di primo grado.
k+3>0 → k>-3
k+4>0 → k>-4
Inseriamo i valori appena trovati su un grafico e ci ricordiamo di considerare come soluzione tutte quelle aree del grafico con linea continua ovunque.
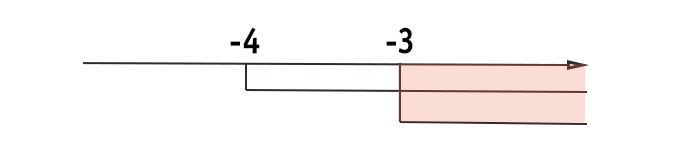
La soluzione è: k>-3
Questo significa che tutti i punti di coordinate P(k+3;k+4) appartengono al primo quadrante quando k è maggiore di -3.
Come esercizio, prova a verifica invece per quali valori di k, il punto appartiene al IV quadrante. Hai dei dubbi? Vorresti proporre un esercizio? Scrivici nei commenti e faremo il possibile per aiutarti.