Un nostro lettore ci chiede: quanto vale il seno di 45°? E’ vero che sulle tabelle e sui formulari di matematica c’è scritto che vale √2/2, ma perché? C’è una dimostrazione valida che giustifichi il risultato di sin45°? – Thomas
Risposta
LA definizione è giusta: il seno di 45 gradi vale √2/2, cioè radical due mezzi (che vale circa 0,707). Possiamo quindi scrivere che:
A volte troverai il valore dell’angolo in radianti, per cui è possibile anche calcolare il seno di 45 esprimendolo nel seguente modo:
senπ/4=√2/2
Se non ricordi come trasformare un angolo espresso in gradi sessagesimali in radianti, dai un’occhiata alla lezione sulla conversione gradi radianti.
Seno di 45, dimostrazione
Iniziamo disegnando la circonferenza goniometrica e staccando su di essa un angolo di 45 gradi.
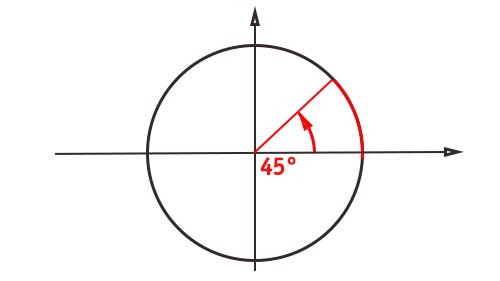
Sulla circonferenza goniometrica andiamo ora a disegnare il segmento orizzontale e verticale partendo proprio dal raggio e che corrispondono (guarda la definizione di seno e coseno) proprio al coseno e al seno di 45 gradi.
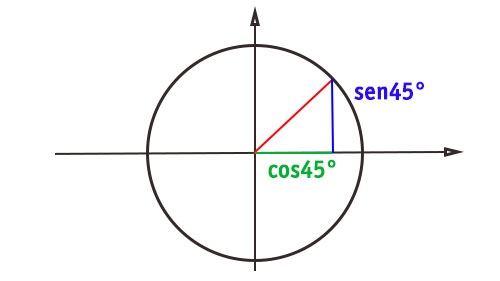
Si nota che il triangolo colorato che abbiamo disegnato è in realtà un triangolo rettangolo isolscele. Questo perché c’è di sicuro un angolo di 90° che si forma tra la linea blu e quella verde. Essendo poi l’angolo che abbiamo disegnato di 45°, l’altro dovrà necessariamente essere pari a 45°.
Questo implica che la linea verde e quella blu, cioè il coseno e il seno di 45°, sono uguali tra loro. Possiamo così applicare il teorema di Pitagora.
sen²α+cos²α=1
(equazione fondamentale della trigonometria)
Perché 1? Perché la circonferenza goniometria è una circonferenza con centro nell’origine e raggio 1. Vuol dire che il segmento rosso disegnato vale proprio 1. Poiché coseno e seno di 45° sono uguali, possiamo anche scrivere:
sen²α+sen²α=1
2sen²α=1
sen²α=1/2
Facciamo a questo punto la radice quadrata a primo e secondo membro…
√(sen²α)=√(1/2)
senα=1/√2
Per rendere il risultato esteticamente più gradevole si esegue una razionalizzazione dei radicali. Quindi moltiplico e divido per radical 2.
senα=√2/2
Abbiamo quindi dimostrato quanto vale il seno di 45. Poiché il coseno è uguale al seno, allora resta univocamente determinato anche il valore di cos45°.
Un piccolo consiglio per lo studente
Il seno di 45 gradi è uno di quei valori di seno e coseno di angoli noti che sarebbe preferibile imparare a memoria. E’ sconsigliabile l’uso della calcolatrice perché nella maggior parte dei casi darà come risultato non radical due mezzi (che è la forma che ci interessa di più), ma 0,717.
Inoltre imparando a memoria questo valore ottenuto, sarà molto più facile andare a lavorare con la determinazione delle funzioni goniometriche (seno, coseno, tangente e cotangente) di angoli più complessi utilizzando gli archi associati.