Hai bisogno di esercitarti con dei problemi sul parallelogramma? Abbiamo raccolto in questa lezione una serie di esercizi e problemi svolti su questa figura geometrica. Troverai molti passaggi commentati, così da agevolartene la comprensione. I problemi sui parallelogrammi sono ordinati per difficoltà crescente, per cui inizia dall’inizio e leggiti con calma i vari metodi di risoluzione.
Conoscenze necessarie per risolvere i problemi
Per poter seguire questa esercitazione è importante che tu conosca le principali formule sul parallelogramma. Durante lo svolgimento dei vari problemi di geometria troverai diversi approfondimenti cliccabili che ti aiuteranno a comprendere le formule e le tecniche utilizzate per arrivare ad una soluzione.
Problemi parallelogramma
Esercizio 1
Un parallelogramma ha un lato che misura 2,6 cm e quello consecutivo 1,4 cm in più del precedente. Calcola la misura del secondo lato.
Svolgimento
AB=2,6 cm
BC=AB+1,4 cm
Si tratta di un esercizio estremamente semplice. Dobbiamo semplicemente calcolare il lato BC ed abbiamo già tutti i dati a disposizione. Per cui possiamo arrivare alla soluzione in un unico passaggio.
BC=AB+1,4=2,6+1,4
BC = 4 cm
Esercizio 2
Il perimetro del parallelogramma misura 390 cm e un lato è il quadruplo dell’altro. Calcolare la misura dei due lati.
p=390 cm
AB=4BC
Svolgimento
Ti ricordi come si calcola il perimetro del parallelogramma? Basta fare la somma dei lati ed essendo uguali i lati opposti, possiamo scrivere:
p=2AB+2BC
Possiamo risolvere il problema sul parallelogramma dividendo il semiperimetro in tanti segmenti tutti uguali tra loro. Quanti? Poiché AB=4BC possiamo dividere in 5 parti uguali (chiamate unità frazionarie).
p/2=AB+BC con BC=1u e AB=4u

A questo punto dividiamo il semiperimetro per le unità frazionarie per ottenere la singola u che è pari proprio a BC.
BC=195/5 = 39 cm
AB= 4×39 = 156 cm
Esercizio 3
Dato il parallelogramma con perimetro pari a 182 cm, un lato supera il suo consecutivo di 21 cm. Calcola la misura dei lati.
p=182 cm
AB=BC+21 cm
Svolgimento
Abbiamo visto che quando c’è il rapporto tra i lati si può usare il metodo delle unità frazionarie. In questo caso invece abbiamo una somma, per cui usiamo un metodo differente per risolvere il problema di geometria sul parallelogramma. In particolare calcoliamo subito il semiperimetro:
p = 2(AB+BC) = 182 cm
p/2=AB+BC=182/2 = 91 cm
A questo punto calcoliamo il lato maggiore attraverso la semisomma del semiperimetro più la differenza tra i due lati. Il lato minore si calcola con la semi-differenza di semiperimetro e differenza tra i lati. Quindi:
AB=(p+21)/2
AB=(p-21)/2
AB=(91+21)/2=56 cm
BC=(91-21)/2=35 cm
Ovviamente questo problema sul parallelogramma poteva essere risolto anche con le equazioni di primo grado, ma generalmente non rientrano ne programmi delle scuole medie.
Esercizio 4
La somma di due lati consecutivi di un parallelogramma è 8 cm e il primo è 2/3 del secondo. Calcola il perimetro e la misura dei lati.
AB+CB=8cm
AB=2/3BC
Svolgimento
Sostanzialmente questo problema di geometria è molto simile al n.2 visto in questa esercitazione. Abbiamo una semisomma e c’è un rapporto tra i lati. Quindi proviamo a risolvere l’esercizio con il metodo delle unità frazionarie.
Poiché AB=2/3BC → 3AB=2BC → AB=3u e BC=2u
AB è uguale a 3 unità frazionarie, mentre BC è uguale a 2 unità. Quanto vale u? Basta dividere l’intero segmento (8 cm) per il numero di unità. Quindi:
u=8 cm/5 = 1,6 cm
AB=2u=3,2 cm
BC=3u=4,8 cm.
Come verifica, si nota che AB+BC è proprio pari a 8 cm per cui il risultato è verificato.
Esercizio 5
Un parallelogramma ha il perimetro di 39 cm, il lato maggiore è il doppio del minore. Calcolare la misura dei due lati.
p=39cm
AB=2BC
Svolgimento
Il procedimento è analogo al precedente, ma non abbiamo più la somma di 2 lati, ma di 4 lati. Per cui invece del perimetro usiamo il semiperimetro.
p=2(AB+BC)=39 cm
p/2=AB+BC=18 cm
A questo punto, poiché AB=2BC, dividiamo il segmento in 3 parti (2 di AB e 1 di BC). AB sarà quindi pari a 1 unità frazionaria, mentre BC=2u. Possiamo quindi calcolare quanto vale l’unità frazionaria.
u=18 cm/3= 6 cm
AB=2u=12 cm
BC=1u = 6 cm.
Esercizio 6
In un parallelogramma, un lato è i 3/5 di quello consecutivo. La loro differenza è invece 16 cm. Calcola la misura dei lati e il perimetro.
AB-CD=16 cm
AB=3/5 cm
Svolgimento
Anche in questo caso dobbiamo usare le unità frazionarie. Questa però non c’è più la somma, ma la differenza. Disegniamo quindi 5 segmenti uguali. Perché proprio 5? E’ il numero al denominatore della frazione. Subito sotto disegniamo 3 segmenti per ottenere CD. Perché proprio 3? E’ il numeratore della frazione.
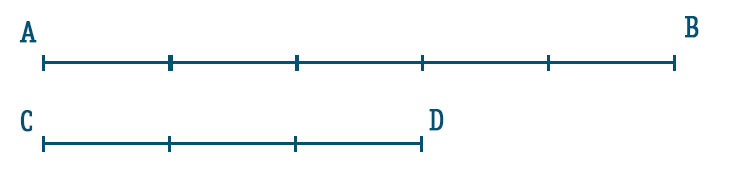
Come puoi notare dal grafico ci sono 2 segmenti di differenza tra AB e CD. Questo significa che AB-CD=2u (unità frazionarie).
Poiché la differenza tra i lati consecutivi del parallelogramma ci viene data dalla traccia ed è pari a 16 cm, allora 2u=16.
Per cui u=8 cm.
A questo punto ricomponiamo i segmenti e scriviamo:
AB=5u=40 cm
CD=3u=24 cm.
Esercizio 7
Un parallelogramma di perimetro 144 cm ha i due lati consecutivi con differenza 12 cm. Calcola la lunghezza di ciascun lato.
2(AB+BC)=144
AB-BC=12 cm
Svolgimento
In questo caso dobbiamo risolvere con il metodo della somma e della differenza tra i lati. Dato che il perimetro è il doppio della somma, calcoliamo il semiperimetro.
p/2=AB+BC=144/2 cm
p/2=77 cm
A questo punto usiamo le formule:
L = lato maggiore = (S+D)/2
l = lato minore = (S-D)/2
AB=(77+12)/2= 44,5 cm
BC=(77-12)/2= 32,5 cm
Nota: le formule viste ora, si ricavano risolvendo un semplice sistema di primo grado con il metodo della somma e della differenza. Questo metodo si studia alle scuole superiori.
Esercizio 8
Il perimetro di un parallelogramma è 436 cm, un lato supera di 26 cm il doppio del suo consecutivo. Calcola la misura dei lati del parallelogramma dato.
2p=436 cm
AB=2BC+26 cm
Svolgimento
Come sempre invece di considerare il perimetro, calcoliamo il semiperimetro, così da ottenere la somma dei due lati consecutivi.
p/2=AB+BC=218 cm
Sempre con il metodo dei segmenti e delle unità frazionarie possiamo disegnare il grafico:
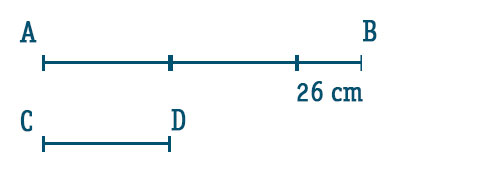
Come puoi vedere consideriamo il segmento CD=1u, mentre il lato BC è uguale al doppio di CD a cui va sommato 26 cm alla fine. Questo vuol dire che la loro somma è:
AB+BC=2u+26cm+1u
AB+ BC=3u+26 cm
Poiché AB+BC=218 cm, allora sottraendo quei 26 cm alla misura del semiperimetro ottengo
218-26=3u
3u=192
u=BC=64
AB=2BC+26=154 cm.