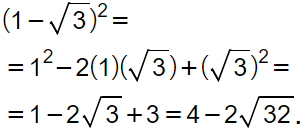Come si svolge la moltiplicazione tra radicali? Ho un esercizio in cui c’è da risolvere una moltiplicazione tra radici ad indice diverso. Come posso risolverla? Potete spiegarmi come farla in maniera semplice? – Grazie Serena
RISPOSTA
Fare le moltiplicazioni tra radicali non è così difficile come gli studenti possono immaginare. A seconda del caso specifico e dell’esercizio, esistono diversi modi e tecniche di calcolo.
Moltiplicazione tra radicali con lo stesso indice di radice
Vuoi un esempio concreto? Dobbiamo risolvere la moltiplicazione tra due radici quadrate. In questo caso la regola è molto semplice:
La moltiplicazione tra radici con lo stesso indice è una radice che ha lo stesso indice e come prodotto il prodotto dei radicandi
![]()
Esempio:
Risolvere la seguente moltiplicazione tra radicali.
![]()
Cosa abbiamo fatto in questo esercizio? La moltiplicazione dei radicandi e poi abbiamo estratto il 3 dalla radice quadrata. Se non ricordi come si fa, leggi i nostri appunti sulle regole e proprietà dei radicali.
Prodotto di radici con indice diverso
La moltiplicazione tra radicali diventa leggermente più difficile nel caso in cui gli indici di radice sono differenti. L’operazione preliminare da eseguire in questo caso è quella di trasformare le radici facendo in modo che abbiano lo stesso indice. Per fare ciò, ecco i passaggi che devi seguire:
- calcola il minimo comune multiplo dei due indici di radice. Se hai ad esempio una radice quadrata e una cubica, allora il mcm è 6.
- le due radici vengono trasformate ed entrambe avranno come indice il mcm e lo stesso argomento, elevato però al rapporto tra mcm e indice di radice.
- a questo punto si tratta di risolvere il caso precedente, cioè una moltiplicazione di radicali con lo stesso indice.
Esempio:
E’ molto più facile mostrarti come si fa attraverso un esercizio svolto. La traccia è sempre la stessa. Calcolare la moltiplicazione tra le radici:
![]()
Come abbiamo detto il primo passo è trasformare le radici in modo che abbiano lo stesso indice e ricondurci ad una moltiplicazione di radicali con stesso indice. Per fare ciò si calcola il minimo comune multiplo tra i due indici: 2 per la prima radice, 3 per la seconda radice. Quindi mcm=6. Poi si calcola:
- 6:2 (primo indice di radice)=3 → 3 è l’esponente da applicare alla prima radice.
- 6:3 (secondo indice di radice)=2 → 2 è l’esponente da applicare alla seconda radice.
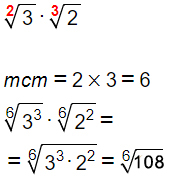
Cosa abbiamo fatto negli ultimi passaggi? Il 36 è diventato 6 elevato al quadrato e poi abbiamo semplificato l’indice di radice con l’esponente.
Esercizi svolti
Oltre agli esempi svolti, che mostrano come calcolare la moltiplicazioni tra radici nei due casi, vogliamo mostrarti qualche caso concreto leggermente più impegnativo. Vediamo allora come comportarci di fronte ad un vero esercizio sul prodotto di radicali.
Esercizio 1)
Il primo esercizio è un’ottima occasione per ripassare anche il prodotto di una somma per una differenza. L’esercizio ci chiede non solo di calcolare la moltiplicazione tra radici, ma semplicemente di risolvere questa espressione algebrica:
(2+√5)(2-√5)
Non è necessario eseguire tutti i passaggi della moltiplicazione tra polinomi. E’ sufficiente moltiplicare i termini uguali tra loro e i segni delle due parentesi.
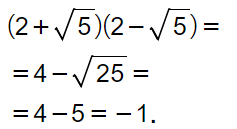
Esercizio 2)
Con il secondo esercizio facciamo anche un ripasso del quadrato di binomio applicato alle radici.