La funzione coseno appartiene alla famiglia delle funzioni trigonometriche, è definita per ogni x appartenente all’insieme dei numeri reali ed è periodica. Tracciando il grafico della funzione coseno, che in matematica viene rappresentata da y=cosx, si ottiene la cosinusoide.
In questa lezione vedremo quali sono le caratteristiche della funzione coseno, il grafico, il dominio, i punti di intersezione e le eventuali simmetrie. Insomma uno studio di funzione completo senza però utilizzare limiti o derivate (che si studiano invece nel programma di analisi)
Grafico della funzione coseno
Per ricavare la cosinusoide si riportano sugli assi cartesiani i valori del coseno compresi tra 0 e 2π. Oltre questo intervallo non conviene andare perché poi si ripetono all’infinito. Disegniamo così la circonferenza goniometrica sulla sinistra e riportiamo il valore del coseno per ogni angolo.
| Angolo (x) | y=cosx |
| 0 | 1 |
| 90° (π/2) | 0 |
| 180° (π) | -1 |
| 270° (3/2π) | 0 |
| 360° (2π) | 1 |
Per disegnare il grafico della funzione coseno y=cosx, facciamo coincidere il punto (0;-1) della circonferenza goniometrica con l’origine O degli assi cartesiani. Sull’asse delle x riportiamo l’ampiezza dell’angolo gradi o radianti, sull’asse delle y l’ascissa di B (cioè la funzione coseno dell’angolo)
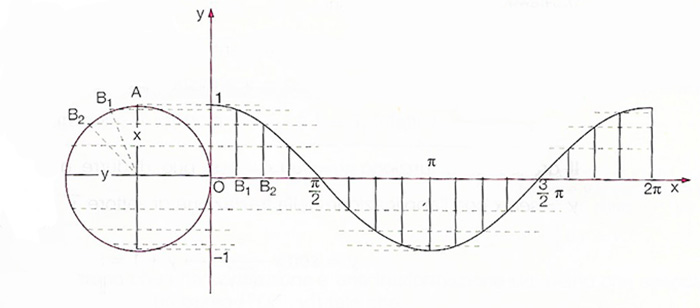
Cosinusoide
Riportando tutti i punti sul grafico di y=cosx con x compreso tra 0 e 2π, si ottiene una curva detta cosinusoide. Questa non è altro che la rappresentazione grafica della funzione coseno sugli assi cartesiani.
La funzione coseno è periodica
La prima cosa che puoi notare è che, analizzando il grafico della funzione coseno, quando la x=0 e quando la x=360° (o 2π), la funzione assume gli stessi valori, cioè la y sul grafico è la stessa. Questo vuol dire che la funzione coseno è periodica con periodo 2π, cioè si ripete in maniera ciclica (sia a sinistra che a destra del grafico) assumendo sempre gli stessi valori.
Possiamo quindi riportare il grafico della funzione coseno anche nella versione completa, cioè riportandone i valori sia a destra che a sinistra di 0 e 2π. Avremo così il disegno della cosinusoide completo.
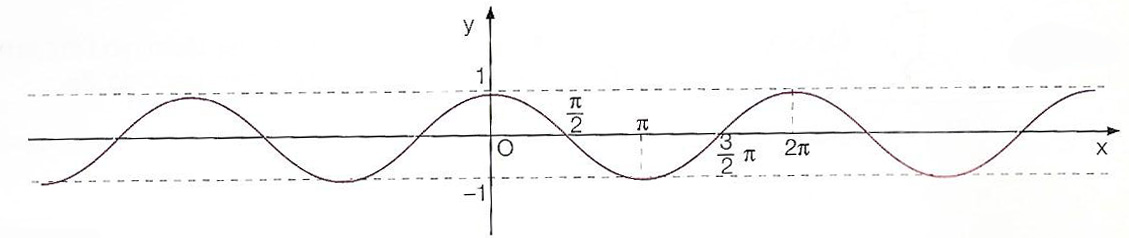
Dominio della funzione coseno
Prova a rispondere a questa domanda guardando la curva cosinusoide. Vedi delle interruzioni sul grafico? Ci sono degli intervalli in cui la funzione si interrompe in qualche modo oppure ti sembra una linea continua che va avanti senza interruzioni? Se dovessi disegnarla non staccheresti mai la penna dal foglio.
Questo significa che la funzione è definita in tutto l’insieme dei numeri reali. Quindi se ti viene chiesto: qual è il dominio della funzione coseno? La risposta è: tutto R, o per essere più rigorosi nel linguaggio matematico, ∀x∈R
Codominio della funzione coseno
Più raramente i docenti si preoccupano di chiedere il codominio delle funzioni, ma è il caso di saperlo. Senza entrare troppo nei dettagli, il codominio ti indica l’intervallo di variazione del grafico in senso verticale. La cosinusoide, come puoi vedere tu stesso dalla figura, non va mai al di sotto di -1 e non va mai al di sopra di +1.
Questo vuol dire che il codominio è l’intervallo chiuso [-1;+1]. Si parla di intervallo chiuso perché i valori -1 e +1 sono compresi e definiti nella funzione.
La funzione coseno è simmetrica?
Continuando la nostra analisi della funzione seno, proviamo a fare un’osservazione. Prova a suddividere il grafico in due parti: la zona a sinistra dell’asse delle y (con x<0) e la zona a destra dell’asse delle x (con x>0). Hai fatto caso che sono praticamente uguali? Questo significa che c’è una simmetria rispetto all’asse y, cioè la funzione coseno è pari.
Quando inizierai a fare lo studio di funzioni, vedrai che questa condizione si dimostra matematicamente perché
f(x)=f(-x)
cioè
cos(x)=cos(-x)
Ad esempio il coseno di 30 è uguale al coseno di -30 (cioè 360-30=330°).
Intersezione con gli assi
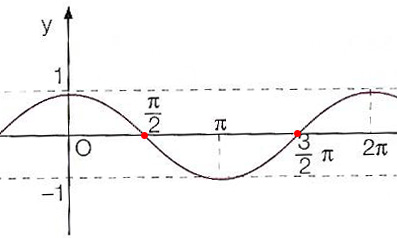
Come puoi vedere dal grafico della cosinusoide, nell’intervallo tra 0 e 2π, la funzione coseno si interseca 2 volte con l’asse delle ascisse. I punti hanno coordinata x=π/2 e x=3/2π. Quindi per gli angoli di 90° e 270° la funzione coseno si annulla. Infatti, analizzando la tabella dei valori di seno e coseno sappiamo che:
- cos90°=0
- cos270°=0
Quindi i due punti di intersezione, che abbiamo segnato in rosso sul grafico sono P1(π/2;0) e P2(3/2π;0). Se volessimo individuare matematicamente questi due valori dovremmo mettere a sistema la funzione coseno y=cosx, con l’equazione della retta y=0 che rappresenta invece l’asse delle ascisse.
Per approfondimenti vedi come calcolare l’intersezione tra due rette (la regola si applica per l’intersezione di due generiche curve, quindi anche della cosinusoide)
Altri spunti per gli esercizi
Molto spesso negli esercizi vengono chieste delle funzioni meno elementari della cosinusoide. Capita quindi di dover studiare la funzione coseno al quadrato o la funzione cos2x o ancora la funzione coseno in valore assoluto. In base a quanto detto fino ad ora è possibile dedurre il grafico di altre funzioni del coseno.
Esempio
Tracciare il grafico, eventualmente approssimato, della seguente funzione coseno → y=cos|x|
Il grafico della funzione coseno valore assoluto si ottiene dalla normale cosinusoide y=cos(x) ribaltando attorno all’asse delle y le parti del grafico che si trovano a destra dell’asse verticale. Proviamo a scrivere i valori di cos|x| al variare dell’angolo x.
| Angolo (x) | y=cos|x| |
| 0 | y=cos(0)=1 |
| -90° (-π/2) | y=cos(90)=0 |
| -180° (-π) | y=cos(-180)=-1 |
| -270° (-3/2π) | y=cos(270)=0 |
| -360° (-2π) | y=cos(360)=1 |

Si può notare che il grafico del coseno in valore assoluto è identico a quello della cosinusoide.