Cosa sono le equazioni esponenziali con basi diverse? Come le risolvo? Se ti sei posto una di queste domande, ecco la lezione adatta a te!
Prima di iniziare: sai cos’è un’equazione esponenziale? Conosci i metodi risolutivi? Se la risposta ad una delle due domande è negativa, ti invito a dare un’occhiata alla lezione sulle equazioni esponenziali. Lì potrai trovare tutte le nozioni necessarie per comprendere pienamente questa nuova lezione.
COSA SONO E COME RICONOSCERLE:
Un’equazione esponenziale con basi diverse è un’equazione esponenziale con due basi numeriche differenti e si presenta in una delle due forme:
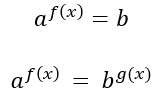
Puoi notare la presenza di esponenziali con basi diverse, a e b.
Nota: non è importante cosa ci sia all’esponente, visto che sono equazioni esponenziali con base diversa anche le equazioni che si presentano nella forma:
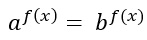
Come vedremo successivamente, questa particolare forma in cui gli esponenti sono uguali ha un metodo risolutivo molto semplice.
Come risolvere le equazioni esponenziali con base diversa
Per poter affrontare esercizi andremo ad applicare le proprietà dei logaritmi e le proprietà delle potenze. Vediamo come si può procedere in maniera semplice ed evitando errori. Partiamo dalla generica forma base in cui ho due esponenziali con la base differente:
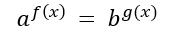
Il primo passaggio è quello di applicare il logaritmo ad entrambi i membri.
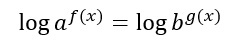
Sfruttando la proprietà dei logaritmi, posso trasformare gli esponenti in coefficienti:
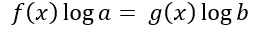
Si prosegue l’esercizio andando a svolgere le moltiplicazioni. Puoi risolvere poi eseguendo raccogliendo la x per ottenere poi un’equazione di primo grado generalmente molto semplice da risolvere.
NOTA: in questo esempio è stato applicato il logaritmo in base decimale, ma nulla vieta di applicare il logaritmo in base a o in base b per rendere ancora più semplice i calcoli. Vedremo tra pochissimo la differenza all’interno di un esercizio.
Regola semplificata con lo stesso esponente
Nel caso in cui ci troviamo a dover risolvere esponenziali con base diversa ma stesso esponente, si ottiene un risultato banale.
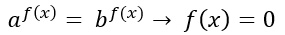
Basta cioè porre la funzione presente all’esponente pari a 0, cioè f(x)=0.
DIMOSTRAZIONE – Ti stai chiedendo il perché? Si dimostra in maniera semplicissima. Prova a dividere primo e secondo membro dell’equazione per b elevato ad f(x)
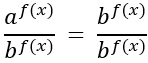
Considerando che al secondo membri hai 1 e che è possibile applicare la proprietà delle potenze (divisione tra potenze con stesso esponente), otteniamo:
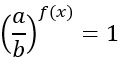
Quest’ultima equazione è vera solo se l’esponente è uguale a zero. Infatti una potenza è sempre uguale ad uno se l’esponente è pari a 0 (purché la base sia diversa da 1). Quindi f(x)=0 è il risultato.
Esercizi con esponenziali con base diversa
Questi esercizi svolti ti aiuteranno ad avere un’idea più chiara e a prendere confidenza con i passi da eseguire.
Esercizio 1
Partiamo con un esercizio semplice:
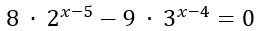
Puoi notare che si tratta di un’esponenziale con basi diverse: sia 2 che 3 sono potenze di x. Come prima cosa devo modificare l’equazione di partenza in modo da renderla più semplice e più vicino alla forma
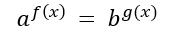
Questo è possibile notando che il numero 8 è la potenza terza di 2 e il numero 9 è proprio 3 al quadrato. Per cui posso riscrivere la traccia come:
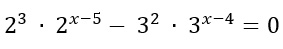
Posso ora applicare le proprietà delle potenze (moltiplicazione tra potenze con stessa base):
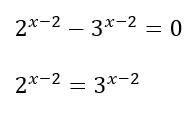
Sono arrivato quindi alla forma base che cercavo: esponenziale a destra e a sinistra ma con basi diverse ma stesso esponente. Quindi possiamo ricorrere alla formula semplificata e porre l’esponente uguale a zero:
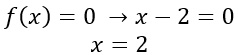
Esercizio 2
Questo esercizio è molto simile al precedente ma mostra un altro metodo per semplificare l’equazione di partenza. I passi da eseguire sono gli stessi.
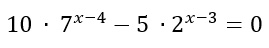
Semplifico l’equazione esponenziale in modo tale da ricondurmi alla forma elementare con i due esponenziali a primo e secondo membro. In questo caso posso dividere per 5 entrambi i membri:
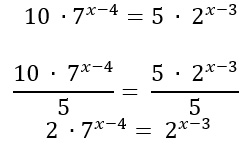
Noto ora che entrambi i membri sono divisibili per 2. Eseguo la divisione:
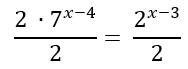
Mentre al primo membro il due si semplifica, al secondo utilizzo ora le proprietà delle potenze (divisione potenze con stessa base):
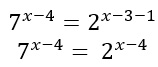
A questo punto, ho raggiunto la forma base con un’equazione esponenziale con basi diverse. Posso risolvere ponendo l’esponente uguale a zero.
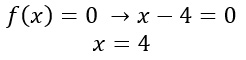
Come puoi notare, una volta raggiunta la forma nota basta semplicemente utilizzare la regola. Passiamo ad esercizi più complessi che prevedono l’utilizzo di esponenziali e logaritmi.
Esercizio 3
Partiamo con un esercizio semplice che ti permetta di capire i passaggi da seguire:
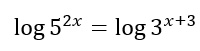
Notiamo la forma di un’equazione esponenziale con basi diverse ed esponenti diversi. I numeri 5 e 3 sono potenze diverse di x (5 è elevato a 2x mentre 3 è elevato a x-3).
METODO 1
Per poter risolvere l’equazione applico il logaritmo ad entrambi i membri:
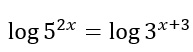
Utilizzo le proprietà dei logaritmi e con una semplice moltiplicazione posso scrivere:
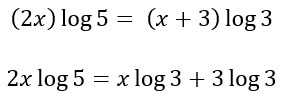
A questo punto posso raccogliere a fattor comune la x,
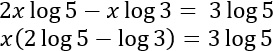
Risolvo l’equazione di primo grado portando al secondo membro la parentesi contenente i coefficienti della x:
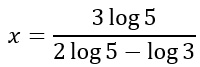
METODO 2 – Che cosa succede se invece di considerare il logaritmo decimale, utilizzo ad esempio il logaritmo in base 5? E’ una scelta che possiamo operare e che non cambia lo svolgimento dell’esercizio.
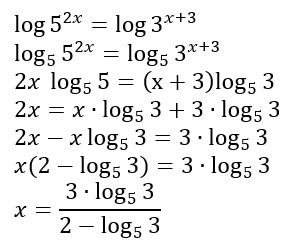
Si dimostra che i risultati dei due metodi sono perfettamente uguali, basta applicare la formula del cambiamento di base dei logaritmi.
ESERCIZIO 4
Quest’ultimo esercizio è analogo al precedente, ma più complesso. Notiamo infatti la presenza di tre esponenziali con base diversa ed esponenti diversi:
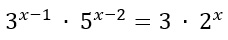
- 3 è elevato ad x-1
- 5 è elevato ad x-2
- 2 è elevato ad x
Come prima cosa applico il logaritmo ad entrambi i membri. Ricordati di utilizzare bene le parentesi per non commettere errori. Al primo membro infatti il logaritmo viene applicato entrambi gli esponenziali:
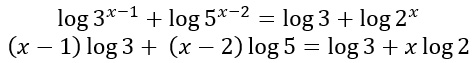
Utilizzo le proprietà dei logaritmi:
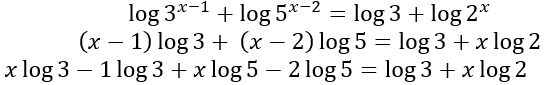
Raccolgo la x:
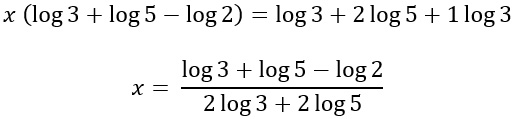
Conclusioni
Abbiamo visto che posso risolvere le equazioni esponenziali con i logaritmi quando mi trovo di fronte a basi differenti. E’ sufficiente applicare il logaritmo ad entrambi i membri e utilizzare poi le proprietà delle potenze. Come hai visto nella risoluzione degli esercizi, i passi da seguire sono sempre gli stessi.
Prova a risolvere la nostra esercitazione sull’argomento. Vai alla pagina degli esercizi sulle equazioni esponenziali.
Se questo articolo ti è stato utile ed è di tuo gradimento, lasciaci un commento in basso. Buona matematica!