Devo risolvere un esercizio che mi chiede di calcolare l’area di un triangolo isoscele noti i lati. Come posso svolgere l’esercizio? Quali formule posso utilizzare? E’ possibile avere anche un esempio pratico? Grazie – Loredana
RISPOSTA
Loredana ci ha esposto un dubbio comune a tanti studenti di matematica che, durante i vari esercizi di geometria, hanno difficoltà a calcolare l’area dei triangoli isosceli. Questo perché utilizzando la formula generale, ovvero base per altezza diviso due, potrebbe non essere immediatamente nota la misura dell’altezza.
Come si svolge l’esercizio se ad esempio si hanno a disposizione i lati del triangolo? I metodi sono due:
- calcolare l’altezza sfruttando il teorema di Pitagora;
- usare la formula di Erone.
Generalmente si preferisce utilizzare il primo metodo perché richiede un po’ di ragionamento in più ed i calcoli sono molto più semplici. Vediamo quindi come si procede.
Calcolare l’area del triangolo isoscele – Metodo 1
Iniziamo subito disegnando un triangolo con due lati uguali e con base AB e altezza CH. Nel caso siano noti i lati, vuol dire che il problema ci darà i lati AB e uno tra AC e BC. In alternativa potrebbe anche fornire la misura di un lato e del perimetro.
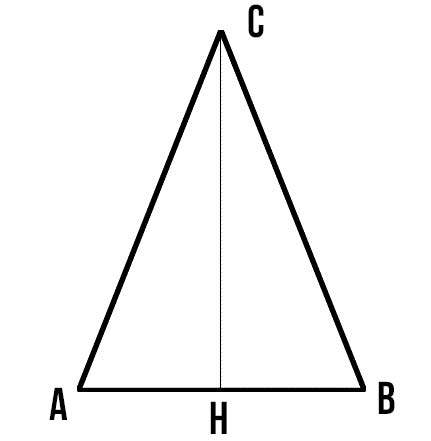
Dovendo calcolare l’area del triangolo isoscele la formula da usare è:
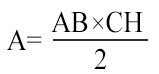
Dobbiamo calcolare l’altezza CH. Come? Considerando il triangolo rettangolo HBC, si nota che CH è il cateto maggiore, HB il cateto minore e BC l’ipotenusa.
Poiché nei triangoli isosceli, l’altezza relativa alla base è anche mediana, CH divide AB in due segmenti uguali, cioè AH=HB=AB/2
Del triangolo rettangolo HBC dobbiamo quindi calcolare il cateto maggiore, avendo ipotenusa e cateto minore. Usiamo quindi il teorema di Pitagora.
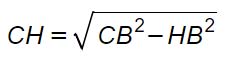
Avendo a disposizione l’altezza, possiamo calcolare l’area del triangolo isoscele con la formula generale che abbiamo già riportato sopra (base×altezza:2) e il problema è risolto. Vediamo un caso pratico, svolgendo assieme un esercizio come esempio.
Esercizi sull’area dei triangoli isosceli
Esercizio 1
Calcolare l’area di un triangolo isoscele che ha perimetro P=18 cm e uno dei lati obliqui è pari a 5 cm.
Per calcolare l’area, ci serve la base. Il problema ci dà la misura del perimetro per cui, facendo la formula inversa del calcolo del perimetro del triangolo isoscele, otteniamo la base.
![]()
![]()
AB=18-2×5=18-10=8 cm
AB= 8 cm
A questo punto, calcolando metà della base, possiamo trovare HB e poi applicare la formula di Pitagora:
HB=AB/2 = 4 cm
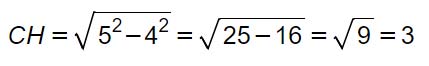
Possiamo a questo punto calcolare l’area del triangolo isoscele come:
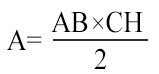
A=8×3:2=12cm².
Esercizio 2
In un triangolo isoscele la base è 1/4 di ciascun lato obliquo. Calcola la misura dell’area del triangolo isoscele dato sapendo che il suo perimetro è di 36,9 cm.
La tendenza di tutti gli studenti che hanno superato le scuole medie (quindi anche dei genitori che mostrano il problema ai figli) è di utilizzare le equazioni con la x come incognita. In effetti ciò porterebbe a risparmiare molto tempo, ma alle scuole medie le equazioni di primo grado non sono state ancora studiate. Per cui si ricorre alle unità frazionarie.
Se la base è 1/4 dei lati obliqui vuol dire che, possiamo disegnare che:
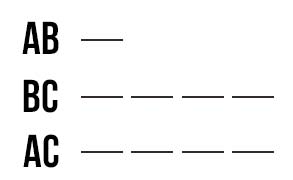
Quindi la base AB è composta da 1 segmento (di cui non sappiamo la lunghezza) e in proporzione i lati obliqui sono composti da 4 segmenti. Poiché la somma di tutti i segmenti ci dà il perimetro, indicando con u=unità frazionaria=lunghezza del segmento
Per cui AB=u e BC=AB=4u
P=1u+4u+4u → P=9u
Facendo la formula inversa, possiamo calcolare:
u=P/9 → u=36,9/9=4,1 cm
Questo vuol dire che
AB=4,1 cm
BC=AB=4,1×4=16,4 cm
A questo punto, noti i lati, possiamo calcolare l’area del triangolo isoscele come mostrato durante questa lezione. Lasciamo a te il completamento dell’esercizio e l’uso del teorema di Pitagora.
Approfondimenti: