Come posso calcolare l’altezza relativa all’ipotenusa di un triangolo rettangolo? Esiste una formula che mi eviti di usare i teoremi di Euclide e di Pitagora? Potreste farmi qualche esempio pratico di calcolo? Grazie – Loredana
Risposta
Loredana ci scrive via mail chiedendoci di chiarire un po’ di dubbi sull’altezza relativa all’ipotenusa. Iniziamo subito vedendo che cos’è e poi qual è la formula più veloce e facile da usare nei problemi.
Che cos’è l’altezza relativa all’ipotenusa
E’ il segmento che unisce perpendicolarmente uno dei vertici con l’ipotenusa.
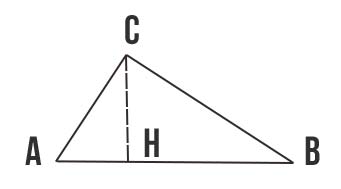
In figura puoi vedere il triangolo ABC, dove AC e BC sono i cateti, mentre AB è l’ipotenusa. Il segmento tratteggiato CH è l’altezza relativa all’ipotenusa.
Formule di calcolo
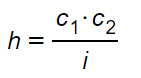
Dimostrazione
Per capire come si arriva a questa formula, riscriviamoci per un attimo le formule per il calcolo dell’area del triangolo rettangolo.
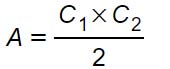
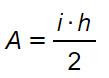
dove c1 e c2 sono i cateti, A è l’area, h è l’altezza relativa all’ipotenusa e i è proprio l’ipotenusa.
Visto che il primo termine è uguale, proviamo ad eguagliare i secondi termini delle due equazioni.
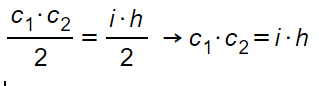
Dopo aver moltiplicato entrambi i membri per 2, semplicemente si sposta la i dell’equazione al primo membro e si ottiene la formula da dimostrare.
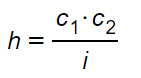
Conclusioni
Abbiamo visto che il metodo più rapido per calcolare l’altezza relativa all’ipotenusa è di sfruttare la misura di tutti i lati del triangolo rettangolo. Per utilizzare la formula vista, infatti, bisogna avere noti sia i cateti che l’ipotenusa. Nel caso in cui i lati a disposizione siano solo 2, si potrà ricavare il terzo applicando il teorema di Pitagora.
Esercizi svolti
Dati i valori dei due cateti 5 cm e 12 cm calcolare, in un triangolo rettangolo, l’altezza relativa all’ipotenusa.

Per utilizzare la formula vista nella parte teorica, ci serve anche l’ipotenusa. Per cui dobbiamo sfruttare il teorema di Pitagora.
AB²=AC²+BC² →AB²=5²+12²=25+144=169
AB=13 cm
Approfondimento: hai notato che il teorema di Pitagora ci porta ad avere un’ipotenusa senza la virgola? Questo perché 5,12 e 13 sono una Terna Pitagorica.
A questo punto possiamo concludere l’esercizio calcolando l’altezza relativa all’ipotenusa.
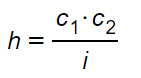
h=12×5:13=4,61 cm
Conclusioni finali
Probabilmente qualche docente non sarà d’accordo ad applicare questa formula perché preferisce applicare i Teoremi di Euclide. Tuttavia ai nostri studenti consigliamo sempre di risolvere i problemi di geometria con il metodo più rapido, semplice e facile da ricordare.
I teoremi di Euclide vanno calcolati quando entrano in gioco anche le proiezioni dei cateti sull’ipotenusa. Altrimenti è più che valida la formula diretta per l’altezza relativa all’ipotenusa che abbiamo visto in questa lezione.