Le terne pitagoriche rispondono ad uno dei quesiti matematici più antichi che si sia mai posto l’uomo: esistono e quali sono i triangoli rettangoli i cui lati hanno lunghezza intera? In questa lezione parleremo del problema delle terne pitagoriche, andandone ad analizzare in maniera semplificata tutte le varie sfaccettature. Iniziamo però subito dando una definizione di terna pitagorica…
Che cosa sono le terne pitagoriche?
Una terna pitagorica è una terna di numeri interi non nulli, per cui vale:
Si parla di terne pitagoriche primitive nel momento in cui, oltre alla condizione precedente, si verifica anche che il massimo comune divisore dei tre numeri sia pari a 1.
Cenni storici
Si parla di calcolo della terna pitagorica perché si attribuisce il problema alla scuola di Pitagora (VI secolo a.C.). Esistono però numerose testimonianze scritte che le terne pitagoriche fossero conosciute già ai tempi dei Babilonesi.
Si tratta di un problema spesso affrontato dai matematici di tutti i tempi e che è stato ripreso in epoca moderna da Sierpinski nel 1962 nel suo testo Pythagorean Triangles. Sull’argomento ci sono tante osservazioni, lemmi e dimostrazioni che potremmo riportare, ma cerchiamo di affrontare l’argomento con il massimo della chiarezza.
Formule per calcolarle
Tutte le terne pitagoriche positive (x,y,z) in cui il primo elemento è pari, possono essere calcolate con la formula:
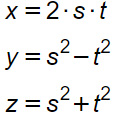
dove s > t sono due numeri interi positivi, con MCD=1, uno pari e l’altro dispari.
Esempio:
Consideriamo i due numeri s=5 e t=4. Sono interi, positivi, con MCD=1, uno pari e l’altro dispari. Per cui applicando la formula vista, si ottiene che:
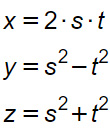
Il trio di numeri (40,9,41) è una terna pitagorica primitiva perché 41²=40²+9² e MCD=1.

Tabella con terne pitagoriche con s che va da 2 a 5.
Come riconoscerle?
Prova a guardare nella tabella sopra le terne pitagoriche più famose che abbiamo segnato. Si notano subito due particolari:
- moltiplicando i primi due elementi della terna pitagorica, si ottiene un numero divisibile per 12;
- moltiplicando i tre elementi della terna pitagorica, si ottiene un numero divisibile per 60.
Quindi puoi riconoscere istantaneamente se 3 valori costituiscono una terna pitagorica, basta verificare che il prodotto dei primi due sia divisibile per 12 e che il prodotto di tutti i valori sia divisibile per 60.
Alcune osservazioni
- Ogni terna pitagorica può essere ottenuta moltiplicando gli elementi della terna per un numero intero.
Esempio:
(3,4,5) è una terna pitagorica intera perché 3²+4²=5² MCD=1. Da notare che (3,4,5) è una delle terne pitagoriche più famose.
Moltiplicando questa terna per un numero intero (ad esempio 2) ottengo:
(3,4,5) → (6,8,10)
Quest’ultima è una terna pitagorica perché 6²+8²=10² mentre il MCD=2 (il numero per cui abbiamo moltiplicato).
- Sia (x,y,z) una terna pitagorica primitiva positiva. Allora se x è pari allora y è dispari e viceversa.
Esempio:
Date le due terne pitagoriche primitive composte da numeri interi positivi (3,4,5) e (8,15,17), si nota che se il primo è dispari il secondo è pari e viceversa.
Esercizi
Si chiama triangolo pitagorico un triangolo rettangolo avente lati di lunghezza intera. Dimostrare che:
- esistono triangoli pitagorici diversi che hanno la stessa area;
- due triangoli equivalenti, formati da lati con misure pari alla terna pitagorica e stessa ipotenusa sono uguali;
- per ogni intero positivo Δ, esiste un numero finito di triangoli pitagorici aventi area uguale a Δ;
Risoluzione
- Iniziamo con il primo punto.
Dobbiamo dimostrare che esistono triangoli pitagorici diversi con la stessa area. Consideriamo ad esempio le due terne pitagoriche (21; 20; 29) e (35; 12; 37). Per calcolare l’area dei due triangoli rettangoli, sapendo che il lato lungo è l’ipotenusa, allora possiamo usare la formula:
A=(Cateto1×Cateto2)/2
A1=20×21/2=210
A2=35×12/2=210
Vuol dire che abbiamo due terne pitagoriche (x,y,z) e (a,b,c) associate ai due triangoli rettangoli. Immaginiamo ad esempio le due terne.
- Per dimostrare il secondo punto, abbiamo due triangoli con la stessa area e stessa ipotenusa, per cui valgono le 4 relazioni:
- x·y/2=a·b/2 →xy=ab , perché hanno stessa area
- z=c , perché hanno stessa ipotenusa
- x²+y²=z²
- a²+b²=c²
Se vale la numero 2, allora possiamo compattare la numero 3 e la 4 riscrivendole come:
![]()
Per la prima relazione scritta, se vale xy=ab, moltiplicando entrambi i membri per 2, otteniamo l’uguaglianza: 2xy=2ab. Questo vuol dire che l’ultima equazione può essere riscritta come:
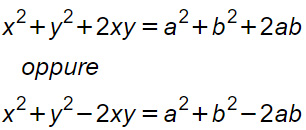
Che possiamo scomporre in quadrati di binomi:
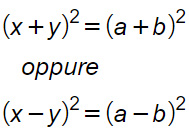
Facendo la radice quadrata a primo e secondo membro, scompaiono le potenze:
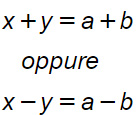
Da questa doppia relazione (puoi risolverla come i sistemi di primo grado con il metodo della somma o della differenza) si ottiene che x=a e y=b. Quindi i due triangoli sono uguali.
- Il terzo quesito ci chiede di dimostrare che esiste un numero finito di triangoli pitagorici con area Δ.
Si dimostra facilmente notando che
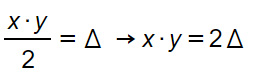
Mentre le terne pitagoriche sono infinite, in questo caso invece abbiamo una possibilità limitata di soluzioni.