I poligoni possono essere classificati in poligoni concavi e convessi. In questa lezione risponderemo in maniera più approfondita alla domanda: che cos’è un poligono concavo?
Ci aiuteremo come sempre con delle figure e attraverso una spiegazione semplificata che possa essere d’aiuto anche agli studenti di tutte le età, anche delle scuole elementari.
Definizione
Si definiscono poligoni concavi tutti quelli che contengono il prolungamento di almeno uno dei lati.
Un aiuto alla comprensione
La definizione è molto simile a quell’angolo concavo, ma generalmente è poco chiara allo studente. Proprio per questa ragione proviamo ad analizzare la figura geometrica seguente.
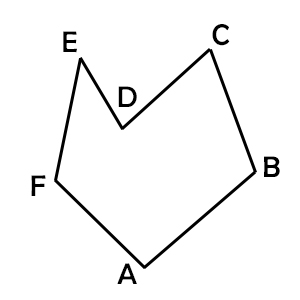
Perché questa figura si definisce un poligono concavo? Per capirlo proviamo a prolungare i suoi lati. Partiamo ad esempio da AB.
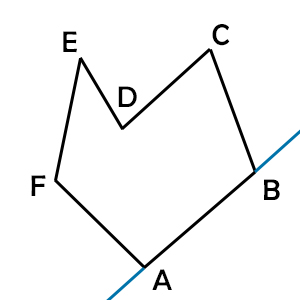
Come puoi vedere il prolungamento del lato AB non interseca mai la figura stessa e resta sempre esterno. Proviamo ora a fare lo stesso con il lato CD.
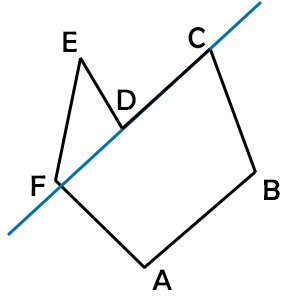
Come puoi vedere il prolungamento del lato CD, sul lato della D, va a tagliare l’interno della figura.
Ecco spiegata la definizione di poligoni convessi: almeno uno dei lati ha il prolungamento interno alla figura.
Quali sono le figure concave?
In genere nel programma di geometria euclidea si studiano i poligoni convessi. Di questi esistono formule più specifiche per calcolarne perimetro ed area. Vuoi un esempio di figura concava?
La stella è un poligono concavo
Caratteristiche e proprietà
Una delle proprietà dei poligoni concavi riguarda l’ampiezza degli angoli interni.
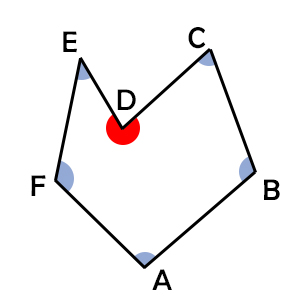
Come puoi notare almeno uno degli angoli ha un’ampiezza superiore a 180°. Questo perché in un poligono concavo almeno uno degli angoli è concavo. E’ possibile che più di un angolo sia concavo, ma non tutti.
Conclusioni
E’ possibile infine stabilire ad occhio se un poligono è concavo o convesso. Basta verificare la presenza di angoli superiori all’angolo piatto (cioè 180°).
Se questa breve lezione ti è stata d’aiuto, lascia un commento positivo. Non ti costa nulla, ma ci aiuterà a crescere e a migliorare la qualità delle lezioni ogni giorno. Per dubbi o perplessità, il nostro staff è a tua disposizione.
Bravissimi