Teoremi di Euclide – formule, definizioni e qualche esempio per metterli in pratica

I due teoremi di Euclide, assieme al teorema di Pitagora, rappresentano i capisaldi della geometria euclidea e permettono di risolvere numerosi problemi che riguardano i triangoli rettangoli.

I teoremi di Euclide devono il loro nome allo scienziato Euclide, vissuto nel 300 a.C. e che raccolse in 12 volumi le regole più importanti della matematica che ancora oggi, dopo più di 2.000 anni, continuiamo ad utilizzare. In questa lezione vedremo quali sono le definizioni dei teoremi di Euclide, sia del primo che del secondo teorema, per poi studiare qualche applicazione pratica.

Generalmente nei programmi di matematica delle scuole medie o delle scuole superiori, si introduce l’argomento spiegando il primo Teorema di Euclide. Con questo si dimostra il Teorema di Pitagora e quest’ultimo viene a sua volta utilizzato per dimostrare il secondo Teorema di Euclide. Iniziamo subito proprio con il primo dei due…

Primo teorema di Euclide

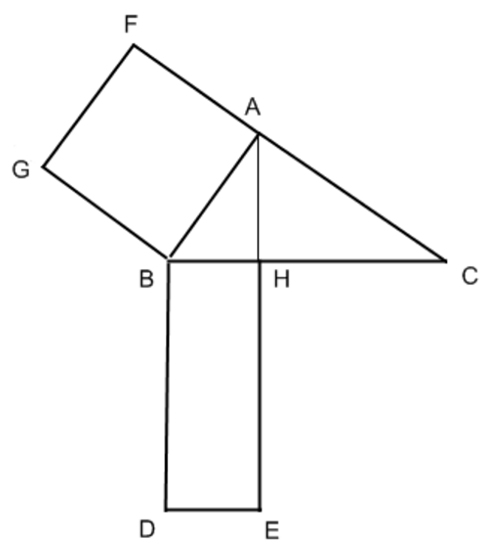
Analizziamo la figura in alto partendo dalla costruzione del triangolo rettangolo ABC, con angolo retto in A. Ecco come procedere per step:

• Si parte disegnando l’altezza relativa all’ipotenusa AH;
• Si disegna il quadrato ABGF sul cateto AB. Quindi per costruzione AB=GB=AF=FG;
• Si traccia un segmento BD perpendicolare a BC e di lunghezza proprio pari a BC. Quindi BD=BC
• Dall’altezza relativa all’ipotenusa si traccia una parallela a BD con la sua stessa lunghezza, quindi EH=BD;
• Infine si chiude il rettangolo BHDE;

Euclide dimostrò che il quadrato ABGF e il rettangolo BHDE sono equivalenti, cioè hanno la stessa area. Quindi la definizione del primo teorema di Euclide può anche essere enunciata come segue:

In un triangolo rettangolo, l’area del quadrato costruita su uno dei cateti è pari all’area del rettangolo che ha per lati la proiezione dell’cateto sull’ipotenusa e l’ipotenusa stessa.

La formula che se ne ricava è quindi:

A_quadrato=A_rettangolo

AB²=BH·BC

Da questa prima formula possiamo anche dire che:

AB·AB=BH·BC

AB:BH=BC:AB

BH:AB=AB:BC

Possiamo quindi dare l’enunciato del primo teorema di Euclide anche nel seguente modo:

In un triangolo rettangolo, un cateto è medio proporzionale tra l’ipotenusa e l’altezza relativa all’ipotenusa.

Secondo teorema di Euclide

In un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per lati le proiezioni dei cateti sull’ipotenusa.

In un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per lati le proiezioni dei cateti sull’ipotenusa.

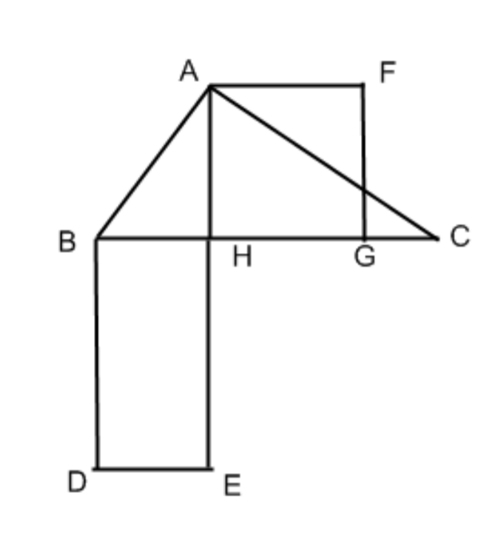
Come per il primo teorema di Euclide, partiamo dall’analisi della figura. Disegniamo il triangolo rettangolo ABC, che ha angolo retto in A. A questo punto procediamo per passi in maniera graduale:

• disegniamo AH, l’altezza relativa all’ipotenusa BC;
• BH e HC sono quindi le proiezioni dei cateti sull’ipotenusa;
• costruiamo il quadrato AHFG che ha per lato l’altezza relativa all’ipotenusa AH;
• quindi per costruzione AH=HG=GF=FA;
• costruiamo il rettangolo BHDE che ha base BH (proiezione del cateto AB sull’ipotenusa BC) e altezza BD (proiezione del cateto AC sull’ipotenusa BC).

Euclide dimostrò che il quadrato AHFG è equivalente al rettangolo BHDE, cioè hanno la stessa area. Quindi si può anche enunciare il secondo teorema di Euclide come segue:

L’area del quadrato costruito sull’altezza relativa all’ipotenusa è uguale all’area del rettangolo che ha per lati le proiezioni dei due cateti sull’ipotenusa.

La formula che se ne ricava è quindi:

A_quadrato=A_rettangolo

AH²=BH·HC

Da questa prima formula possiamo fare qualche semplice passaggio algebrico:

AH·AH=BH·HC

AH:BH=HC:AH

BH:AH=AH:HC

Da quest’ultima formula possiamo ricavare l’ultimo enunciato del secondo teorema di Euclide.

In un triangolo rettangolo, l’altezza relativa all’ipotenusa è medio proporzionale tra le proiezioni dei cateti sull’ipotenusa.

Esempi su come usare i teoremi di Euclide

ESERCIZIO 1 – Calcolare il perimetro di un triangolo rettangolo che ha un cateto pari a 20 cm e la sua proiezione sull’ipotenusa è 14 cm (Difficoltà ★☆)

ESERCIZIO 2 – In un triangolo rettangolo, l’ipotenusa misura 100 cm e le proiezioni dei cateti sull’ipotenusa sono una i 16/9
dell’altra. Calcola perimetro e area del triangolo. (Difficoltà ★★)

SOLUZIONE ESERCIZIO 1

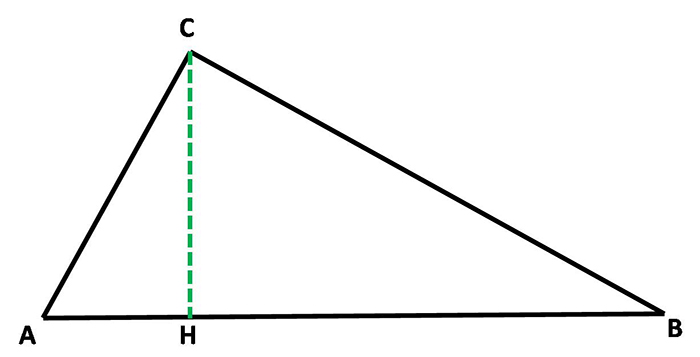
Dati del problema:
AC=20cm
AH=10 cm

Incognite da calcolare: perimetro=?

Con i dati a disposizione possiamo subito applicare il primo teorema di Euclide. Ricordiamoci l’enunciato: in un triangolo rettangolo, un cateto è medio proporzionale tra l’ipotenusa e la proiezione del cateto sull’ipotenusa.

Visto che noi abbiamo il cateto e la proiezione del cateto sull’ipotenusa, applicando la formula inversa dei teoremi di Euclide (in particolare del primo) possiamo quindi calcolarci l’ipotenusa. Dalle formula risulta infatti:

AB:AC=AC:AH
(I teorema Euclide)

In neretto lasciamo solo le incognite:

AB/AC=AC/AH

Isoliamo al primo membro (cioè a sinistra dell’uguale) l’incognita AB:

AB=AC·AC/AH

AB=40·40/4=28,57 cm

A questo punto, per calcolare il perimetro, mi manca solo il secondo cateto. Posso semplicemente applicare il teorema di Pitagora. Considerando infatti il triangolo rettangolo ABC, conosco il cateti AC e l’ipotenusa AB, per cui:

CB=√(AB²-AC²)

CB=√(28,57²-20²)=√416,28

CB= 20,4 cm

Posso a questo punto calcolare il perimetro come la somma dei due cateti e dell’ipotenusa:

p=AB+BC+CA

p=28,57+20,4+20=68.97 cm

SOLUZIONE ESERCIZIO 2

Dati del problema:

AB=100cm

HB=16/9 di AH

Incognite del problema: perimetro ed area=?

Non abbiamo numeri certi in questo problema se non l’ipotenusa. Sostanzialmente ci sono due modi per risolvere il problema: come si fa alle scuole medie e come si fa alle scuole superiori. Vediamoli entrambi…

Come si fa alle scuole medie… 

Dato il rapporto 16/9 ne calcoliamo la somma, cioè 16+9=25. La somma delle due proiezioni è proprio l’ipotenusa, pari a 100cm. Questo vuol dire che il rapporto tra il totale (100) e la somma del rapporto (25) è: 100:25=4.

A questo punto calcolo AH come 9×4=36 cm mentre HB=16×4=64. Si nota che la loro somma è proprio 100.

Come si fa alle scuole superiori…

Dato che HB=(16/9) AH, si pone AH=x, per cui:

HB=(16/9)x

AH+HB=100 → (16/9)x+x=100 → (25/9)x=100 → x=100·9/25=36

AH=36 cm e HB=100-36=64 cm

A questo punto il procedimento è unico sia per le scuole medie che superiori. Abbiamo l’ipotenusa e le due proiezioni. Applichiamo quindi il secondo teorema di Euclide:

In un triangolo rettangolo, l’altezza relativa all’ipotenusa è medio proporzionale tra le proiezioni dei cateti sull’ipotenusa.

AH:CH=CH:HB

Segniamo in grassetto ciò che non conosciamo.

AH:CH=CH:HB → vuol dire che possiamo calcolarci quindi l’altezza relativa all’ipotenusa.

CH·CH=HB·AH → CH=√(HB·AH)=√(64·36)=48cm

A questo punto possiamo procedere in due diversi modi: si possono calcolare con il Teorema di Pitagora i due cateti considerando i triangoli AHC e CHB. La strada più semplice è però senza dubbio quella di calcolare l’area dei due triangoli appena elencati perché di entrambi, se ci rifletti un attimo, hai sia base che altezza. Per cui:

A_AHC=AH·CH/2=36·48/2=864 cm²

A_AHC=HB·CH/2=64·48/2=1534 cm²

Sommando le due aree si ottiene l’area totale del triangolo ABC → A=864+1543=2.407 cm²

Conclusioni sui teoremi di Euclide

Dalla lezione abbiamo quindi appreso una serie di punti fermi importantissimi per risolvere gli esercizi:

• i teoremi di Euclide si applicano solo ai triangoli rettangoli, non a quelli scaleni o isosceli;
• le formule dei teoremi di Euclide hanno sempre come riferimento l’altezza relativa all’ipotenusa;
• con le formule inverse dei teoremi di Euclide, si può calcolare praticamente tutto di un triangolo rettangolo.