Le disequazioni fratte di primo grado sono delle disequazioni che hanno un monomio o un polinomio al denominatore. Sui libri e a scuola vengono spesso insegnate diverse tecniche per risolverle, tuttavia noi preferiamo illustrarti un nostro metodo infallibile e molto più semplice.
La regola che troverai illustrata passo passo vale anche per le disequazioni fratte di secondo grado, per cui una volta appresa, potrai applicarla in qualsiasi tipo di esercizio. Iniziamo subito vedendo che cosa sono e quali sono le disequazioni frazionarie.
Quali sono le disequazioni fratte?
Vi ricordate la lezione sulle equazioni fratte? Il ragionamento è perfettamente analogo: si parla di disequazioni fratte di primo grado se la variabile x appare in almeno un denominatore. Può essere espressa nella forma:
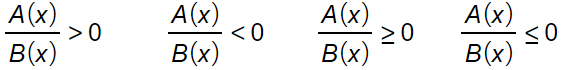
Disequazioni fratte – i 4 casi possibili
Sostanzialmente, quando dobbiamo svolgere esercizi con le disequazioni fratte, il nostro compito sarà di effettuare calcoli o semplificazioni al fine di riportarci a questa forma base. Arrivati a questo, poi, ci sono poche semplici regole da seguire. Vediamole subito.
Come risolvere le disequazioni fratte di primo grado?
Senza entrare troppo nel merito della teoria, proviamo a darti una spiegazione molto pratica sulle disequazioni frazionarie. Il ragionamento vale sia per le disequazioni di primo grado che per quelle di secondo grado.
Si impone un falso sistema (diverso quindi dal sistema di disequazioni), cioè iniziamo a risolvere in due momenti separati il numeratore e il denominatore. Ciascuna soluzione che andremo così ad individuare sarà inserita sul grafico a cui bisognerà aggiungere uno studio del segno. Vediamo subito un esempio su come risolvere le disequazioni di primo grado fratte.
Imponiamo subito numeratore N e denominatore D imponendoli maggiori di 0.

Bisogna imporre N>0 e D>0 qualsiasi sia il verso della disequazione fratta. Sia che ci sia minore che maggiore di 0 vanno comunque imposti maggiori (o maggiori e uguali di 0).
NOTA BENE
Nell’eventualità in cui dobbiamo imporre maggiore e uguale di zero, attenzione: al denominatore non va mai aggiunto l’uguale per alcuna ragione (al denominatore non bisogna mai inserire il segno uguale). E’ questo uno degli errori più frequenti durante i compiti in classe di matematica.
Le due soluzioni che abbiamo trovato vanno imposte sul grafico così come in figura:
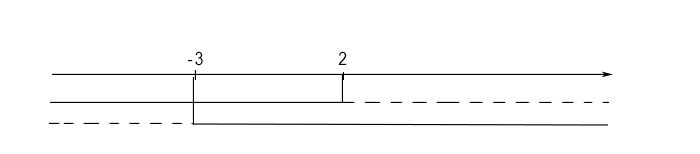
Si mette linea continua dove vale la soluzione trovata, sul resto linea tratteggiata.
A questo punto possiamo studiare il segno, tenendo a mente che linea continua=+, linea tratteggiata= –.
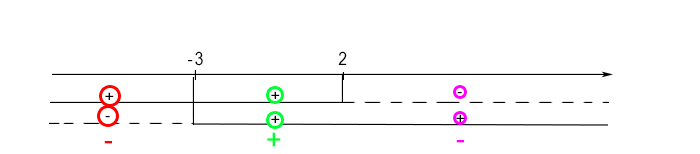
Studio del segno
Abbiamo cioè individuato 3 campi. In ciascuno di questi si moltiplicano i segni corrispondenti. Nel primo abbiamo moltiplicato “più” per “meno” e ottenuto “meno”.
Nel secondo abbiamo moltiplicato “più” per “più” e ottenuto “più”.
Nel terzo abbiamo moltiplicato “meno” per “più” e ottenuto “meno”.
Di questi, poiché la nostra disequazione all’inizio imponeva N/D<0 (vedi la traccia dell’esempio), prenderò tutti i segni negativi, cioè quelli corrispondenti al primo e al terzo campo. Quindi le soluzioni sono:
x<-3 U x>2
Ho cosi preso le soluzioni corrispondenti al primo e all’ultimo campo. L’esercizio è così concluso. A questo punto proviamo a risolvere altri esercizi svolti sulle disequazioni di primo grado.
[adrotate banner=”4″]
Disequazioni fratte di primo grado esercizi svolti
- Di questo primo esercizio vediamo che non ci troviamo subito nella situazione N/D>0 (o N/D<0). Sarà nostro compito quindi portare tutto a primo membro e poi calcolare il minimo comune multiplo. Vediamo come risolvere:
 A questo punto ci siamo trovati nella formula generale delle disequazioni frazionarie: numeratore fratto denominatore e al secondo membro lo zero. Solo a questo punto posso applicare la regola N>0 e D>0.
A questo punto ci siamo trovati nella formula generale delle disequazioni frazionarie: numeratore fratto denominatore e al secondo membro lo zero. Solo a questo punto posso applicare la regola N>0 e D>0.
 Nella disequazione frazionaria risolta abbiamo inserito sul grafico i valori delle due disequazioni e studiato il segno. Poiché ci siamo trovati N/D>0 allora abbiamo preso tutti i valori positivi. La soluzione della disequazione è minore quindi di -3/2 e maggiore di 0, cioè proprio in corrispondenza dei segni +.
Nella disequazione frazionaria risolta abbiamo inserito sul grafico i valori delle due disequazioni e studiato il segno. Poiché ci siamo trovati N/D>0 allora abbiamo preso tutti i valori positivi. La soluzione della disequazione è minore quindi di -3/2 e maggiore di 0, cioè proprio in corrispondenza dei segni +. - Con questo problema vediamo come risolvere disequazioni fratte di primo grado con esercizi più complessi. Dobbiamo sempre ricordare che il primo passo, come già detto con gli esercizi sulle equazioni fratte, è di scomporre i denominatori il più possibile. Quindi cerchiamo di non dimenticare le regole sulle scomposizioni.

Attenzione alle scomposizioni dei denominatori delle disequazioni frazionarie!
Per il primo denominatore abbiamo usato la regola della messa in evidenza parziale, mentre per la seconda una totale. Evitiamo invece di scomporre i numeratori, non aiuterebbe lo svolgimento dell’esercizio e ci farebbe solo sprecare tempo. Possiamo così proseguire:

Ma non è una disequazione fratta di primo grado!!

Scomponiamo il numeratore
Siamo ora nella forma N/D con al secondo membro lo 0. Potremmo già trattare separatamente numeratore e denominatore. Il problema è che al numeratore abbiamo una disequazione di terzo grado che non sappiamo ancora come affrontare! Come risolvere la disequazione fratta che si è presentata? Proviamo a scomporre il numeratore e vedere se qualcosa può essere semplificato con il denominatore: ci ridurrebbe molto i calcoli.
 Anche se numeratore e denominatore non possono essere semplificati possiamo risolvere l’esercizio perché riconducibile ad una disequazione fratta di primo grado. Vale infatti la seguente regola:
Anche se numeratore e denominatore non possono essere semplificati possiamo risolvere l’esercizio perché riconducibile ad una disequazione fratta di primo grado. Vale infatti la seguente regola:
Attenzione: questa regola è fondamentale!
Quando siamo in presenza di un esercizi sulle disequazioni di primo grado con dei fattori (cioè delle parentesi o anche elementi singoli che si moltiplicano tra loro), si pone ciascuno maggiore (o uguale, tranne il denominatore che non vai posto uguale) di 0 e poi si mette sul grafico.
In questo modo possiamo risolvere gli esercizi riconducibili alle disequazioni di primo grado. Proseguendo con il nostro esercizio, infatti, moltiplicando tutto per due abbiamo:
 La seconda e l’ultima disequazione sono di secondo grado. Non abbiamo ancora studiato l’argomento ma possiamo dire che quando siamo in presenza di un numero addizionato alla x al quadrato maggiore di zero, il risultato è sempre verificato (un numero positivo più un’incognita positiva darà sempre risultato positivo). Per cui visto che la soluzione è sempre verificata possiamo mettere linea continua.
La seconda e l’ultima disequazione sono di secondo grado. Non abbiamo ancora studiato l’argomento ma possiamo dire che quando siamo in presenza di un numero addizionato alla x al quadrato maggiore di zero, il risultato è sempre verificato (un numero positivo più un’incognita positiva darà sempre risultato positivo). Per cui visto che la soluzione è sempre verificata possiamo mettere linea continua.
 Il risultato finale come sempre è legato alla forma N/D che abbiamo individuato. Nell’ultima frazione scritta infatti c’era un minore e uguale, per cui il risultato andrà preso con il segno meno. Intenzionalmente abbiamo potuto omettere i due valori sempre verificati, perché non avrebbero influenzato il risultato finale.
Il risultato finale come sempre è legato alla forma N/D che abbiamo individuato. Nell’ultima frazione scritta infatti c’era un minore e uguale, per cui il risultato andrà preso con il segno meno. Intenzionalmente abbiamo potuto omettere i due valori sempre verificati, perché non avrebbero influenzato il risultato finale.
Disequazioni di primo grado esercizi da svolgere
Abbiamo potuto vedere che sulle disequazioni di secondo grado, prendendo un esercizio più complesso, c’è davvero “da divertirsi”. E’ necessario ricordare bene le regole sulle scomposizioni ed allenarsi e fare molta pratica. Per cui vi consigliamo di esercitarvi con le seguenti disequazioni frazionarie di primo grado:
Risolvi le seguenti disequazioni di primo grado superiori al primo intere o fratte, riconducibili allo studio di disequazioni di primo grado.
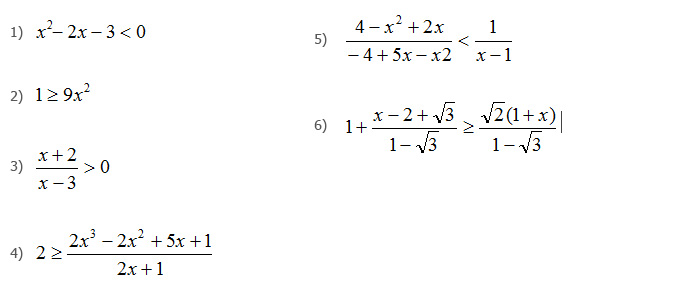
Hai un compito in classe e sei preoccupato? Vuoi un approfondimento o hai ancora dubbi sulle disequazioni di primo grado? Esponi le tue domande scrivendo al nostro staff. Contattaci!
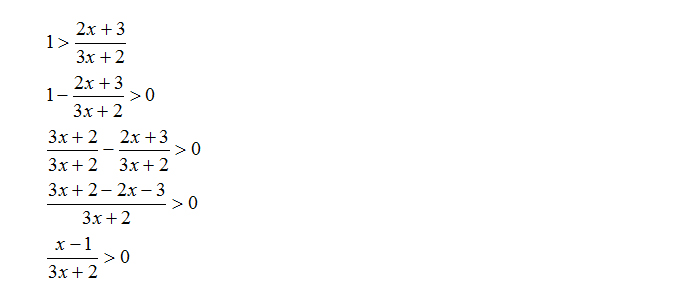 A questo punto ci siamo trovati nella formula generale delle disequazioni frazionarie: numeratore fratto denominatore e al secondo membro lo zero. Solo a questo punto posso applicare la regola N>0 e D>0.
A questo punto ci siamo trovati nella formula generale delle disequazioni frazionarie: numeratore fratto denominatore e al secondo membro lo zero. Solo a questo punto posso applicare la regola N>0 e D>0.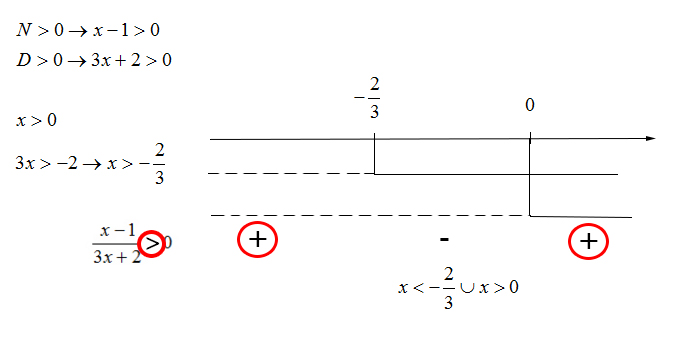 Nella disequazione frazionaria risolta abbiamo inserito sul grafico i valori delle due disequazioni e studiato il segno. Poiché ci siamo trovati N/D>0 allora abbiamo preso tutti i valori positivi. La soluzione della disequazione è minore quindi di -3/2 e maggiore di 0, cioè proprio in corrispondenza dei segni +.
Nella disequazione frazionaria risolta abbiamo inserito sul grafico i valori delle due disequazioni e studiato il segno. Poiché ci siamo trovati N/D>0 allora abbiamo preso tutti i valori positivi. La soluzione della disequazione è minore quindi di -3/2 e maggiore di 0, cioè proprio in corrispondenza dei segni +.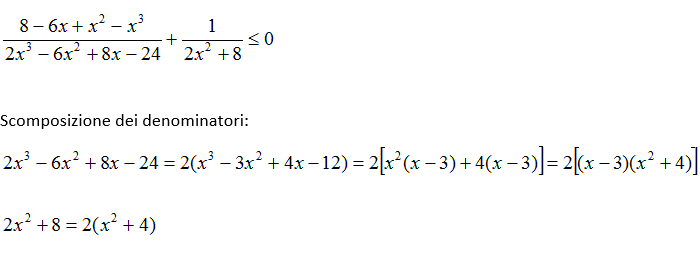

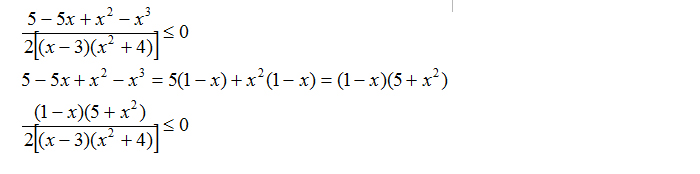

 La seconda e l’ultima disequazione sono di secondo grado. Non abbiamo ancora studiato l’argomento ma possiamo dire che quando siamo in presenza di un numero addizionato alla x al quadrato maggiore di zero, il risultato è sempre verificato (un numero positivo più un’incognita positiva darà sempre risultato positivo). Per cui visto che la soluzione è sempre verificata possiamo mettere linea continua.
La seconda e l’ultima disequazione sono di secondo grado. Non abbiamo ancora studiato l’argomento ma possiamo dire che quando siamo in presenza di un numero addizionato alla x al quadrato maggiore di zero, il risultato è sempre verificato (un numero positivo più un’incognita positiva darà sempre risultato positivo). Per cui visto che la soluzione è sempre verificata possiamo mettere linea continua.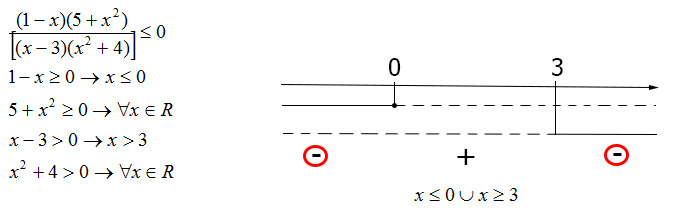 Il risultato finale come sempre è legato alla forma N/D che abbiamo individuato. Nell’ultima frazione scritta infatti c’era un minore e uguale, per cui il risultato andrà preso con il segno meno. Intenzionalmente abbiamo potuto omettere i due valori sempre verificati, perché non avrebbero influenzato il risultato finale.
Il risultato finale come sempre è legato alla forma N/D che abbiamo individuato. Nell’ultima frazione scritta infatti c’era un minore e uguale, per cui il risultato andrà preso con il segno meno. Intenzionalmente abbiamo potuto omettere i due valori sempre verificati, perché non avrebbero influenzato il risultato finale.