Equazioni di primo grado fratte – esercizi svolti

In questa lezione vedremo una serie di esercizi sulle equazioni fratte di primo grado. Analizzeremo quali sono gli esercizi e le espressioni più comuni che si trovano durante i compiti in classi. Potrai allenarti sia con gli esercizi svolti in cui ci sono i vari passaggi e la soluzione che con la lista degli esercizi da risolvere per casa.

Equazioni fratte esercizi

Riassumiamo quanto detto nella lezione sulle equazioni fratte di primo grado. Ecco come si risolvono passo passo:

• sulla colonna destra si impongono le condizioni di esistenza, cioè ogni denominatore deve essere imposto diverso da 0 e si risolve l’equazione che ne deriva.
• si torna sulla parte sinistra della pagina e si calcola il minimo comune multiplo tra i monomi o i polinomi al denominatore.
• tutte le frazioni hanno ora il mcm al denominatore, mentre al numeratore si eseguono i classici calcoli che si fanno con le frazioni
  (mcm : denominatore × numeratore)
• avendo già esplicitato le condizioni di esistenza, posso eliminare tutti i denominatori.
• ho ottenuto così un’equazione da grado 1 che andrò a risolvere con i metodi di svolgimento delle equazioni di primo grado.
• verifica infine che le soluzioni dell’equazione fratta siano compatibili con le condizioni di esistenza.

Nel caso in cui, dopo aver eliminato i denominatori, ti ritrovi con un’equazione di secondo grado, puoi risolvere utilizzando le tecniche viste nella lezione sulle equazioni fratte di secondo grado.

Equazioni fratte esercizi svolti

Proviamo ora a risolvere assieme 3 equazioni di primo grado fratte. La traccia è:

Risolvere le equazioni fratte a coefficienti numerici di seguito riportate:

Esercizio 1

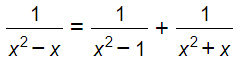
Svolgimento

Vengono chiamate equazioni numeriche fratte perché i coefficienti dei termini noti saranno tutti dei numeri. Non vanno confuse con le equazioni letterali fratte, che hanno un livello di difficoltà leggermente più alto.

Quando ci troviamo di fronte ad esercizi di equazioni fratte di primo grado dove al denominatore ci sono termini di secondo grado – ma anche di terzo, quarto e così via – cerchiamo sempre di usare le regole valide per la scomposizione di polinomi. L’obiettivo è ottenere denominatori più o meno simili in modo di ridurre drasticamente i calcoli necessari per risolvere l’equazione.

In questo caso possiamo utilizzare la messa in evidenza totale nella prima e nell’ultima frazione, mentre nella seconda, essendoci una sottrazione di due termini al quadrato, posso scomporre come il prodotto di una somma per una differenza. Se non ricordi queste regole ti consigliamo di rivedere la lezione sulla scomposizione di polinomi.

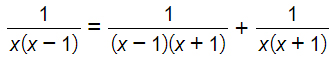
A questo punto posso calcolare il mcm tra i polinomi considerando tutti i termini in parentesi e fuori, presi una sola volta con il massimo esponente.

mcm=x(x+1)(x-1)

A questo punto possiamo scrivere le condizioni di esistenza. Ovvero:

CE: x(x+1)(x-1)≠0

Risolviamo questa semplice equazione ricordandoci la legge dell’annullamento del prodotto:

(A)·(B)·(C)=0 → A=0;  B=0;  C=0

Posso così risolvere le condizioni di esistenza:

x≠0;  x≠±1

Dovremo quindi verificare che tra le soluzioni finali non ci siano questi tre risultati. Torniamo ora al minimo comune multiplo:

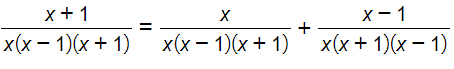
Avendo già esplicitato le condizioni di esistenza, possiamo eliminare i denominatori. Considerando solo i numeratori ottengo la semplice equazione:

x+1=x+x-1

Poiché a sinistra e destra ho lo stesso termine cioè una x, posso eliminarle e scrivere:

1=x-1 → -x=-1-1 → x=2

La soluzione è accettabile perché non coincide con le condizioni di esistenza.

Come abbiamo potuto vedere l’unica vera difficoltà degli esercizi sulle equazioni di primo grado fratte è, oltre alla scrittura delle condizioni di esistenza, il calcolo del minimo comune multiplo tra polinomi.

Esercizio 2

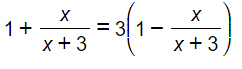
In questo nuovo esercizio sulle equazioni di primo grado, l’unica difficoltà che abbiamo aggiunto è una semplice parentesi tonda con una moltiplicazione. Risolviamola subito:

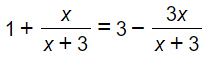
Essendoci tutti termini di primo grado, non è necessario effettuare la scomposizione di polinomi. Per cui posso calcolare direttamente il mcm che in questo caso è banalmente x+3. Individuo così subito le condizioni di esistenza e poi vado avanti con l’esercizio.

CE: x+3≠0 → x≠-3

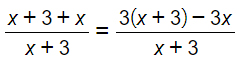
Avendo calcolato le condizioni di esistenza posso eliminare i denominatori ed iniziare a risolvere le prime operazioni di addizione e moltiplicazione ai due membri delle equazione fratta.

2x+3=3x+9-3x

2x=9-3 → x=3

La soluzione è accettabile perché diversa dalle condizioni di esistenza.

Esercizio 3

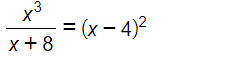
L’ultimo esercizio non presenta particolari difficoltà. Non lasciamoci infatti distrarre dal fatto che compare un termine di terzo grado. Dato che stiamo imparando a risolvere le equazioni di primo grado fratte, andrà certamente via durante i calcoli. Iniziamo risolvendo il quadrato di binomio:

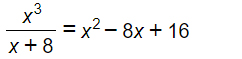
A questo punto come sempre calcoliamo in mcm che in questo caso banalmente è pari a x+8 e, sulla destra del foglio, ci riportiamo le condizioni di esistenza.

CE: x+8≠0 → x≠-8

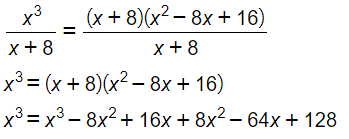
Nell’ultimo passaggio abbiamo semplicemente eseguito una moltiplicazione tra polinomi. Elimino tutti i termini che compaiono uguali al primo e al secondo membro o che troviamo addizionati e sottratti allo stesso membro. Per cui otteniamo:

0=+16x-64x+128

16x-64x+128x=0

-48x=128 → 48x=-128

x=128/48 → x=8/3

Esercizi da risolvere

Ecco un elenco di esercizi sulle equazioni di primo grado fratte che puoi provare a risolvere da solo.

Se vuoi continuare ad allenarti, ti consigliamo gli esercizi sulle equazioni fratte che puoi trovare su questa pagina dell’Università di Bologna. In alternativa troverai tanti altri esercizi sul libro Matematica Bianco – Equazioni e Disequazioni di Primo Grado.