Come si calcolano le potenze di monomi? Esiste una regola che permetta di risolvere gli esercizi in maniera semplice e veloce?
A tutte queste domande rispondere in questa lezione attraverso una semplicissima lezione al termine della quale troverai diversi esercizi svolti. Ovviamente diamo per scontato che tu conosca la definizione di monomio e che sappia quindi qual è la parte numerica e quale quella letterale.
Calcolare potenze di monomi
![]()
La potenza di un monomio sfrutta le proprietà delle potenze, applicando queste ultime alla parte letterale. Andiamo però con ordine e diamo subito un metodo che ci aiuti a risolvere qualsiasi tipo di potenza di monomi.
La potenza di un monomio si esegue elevando all’indice di potenza:
- il segno
- la parte numerica
- la parte letterale
Elevazione del segno
Qui non ci sono calcoli da fare. Ricordati una semplice regola: se l’indice di potenza è pari, il segno sarà sempre positivo. Se l’indice di potenza è dispari, allora il segno resta invariato.
Ad esempio il segno “meno” elevato al quadrato, diventa “più”, mentre elevato al cubo resta negativo.
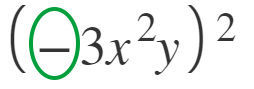
Nell’esempio in figura, poiché l’indice dell’esponente è pari (perché è 2), allora il segno finale sarà necessariamente positivo “+”.
Potenza della parte numerica di un monomio
In questa seconda fase, semplicemente bisogna svolgere semplicemente la potenza del numero, così come ci hanno insegnato nelle scuole elementari.
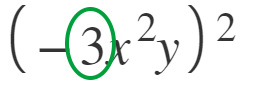
Nell’esempio in figura 3 alla seconda diventa 9. (per approfondimenti puoi consultare la nostra lezione sull’elevamento a potenza)
Potenza di un monomio: la parte letterale
E’ qui che andremo ad applicare le regole sulle potenze. Si considera ogni singola lettera e si moltiplica il suo esponente per quello della potenza.
Vuoi approfondire la regola precisa utilizzata? Leggi la lezione sulla potenza di potenza.
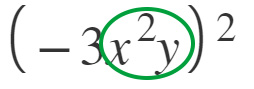
Per cui la x che è già elevata a 2 avrà all’esponente 2×2=4, mentre la y che ha esponente 1, avrà esponente finale 1×2=2.
Il risultato finale della potenza di monomio in esempio è quindi:
![]()
Utilizzando la regola vista in questa prima parte di lezione è possibile risolvere qualsiasi esercizio dai più semplici sino alle espressioni di monomi con potenze.
Potenze di monomi esercizi svolti
Esercizio 1
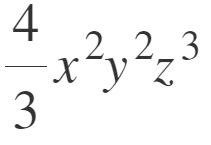
Proviamo ad eseguire il quadrato di questo monomio con frazione. Non essendoci segno negativo, il segno resta positivo, per cui possiamo passare direttamente al calcolo della parte numerica e poi letterale.
Si eleva quindi 4/3 alla seconda, poi la x, poi la y e infine la z. Il risultato che si ottiene è:
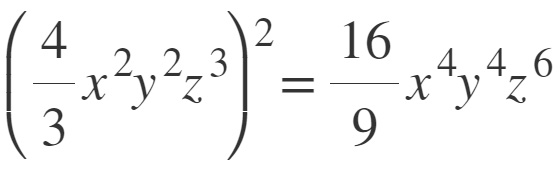
Esercizio 2
Proviamo ora qualcosa di più difficile: elevare a potenze negative. La regola generale la conosciamo già: il meno all’esponente diventa “più” semplicemente invertendo numeratori e denominatori.
Proviamo a risolvere il seguente esercizio.
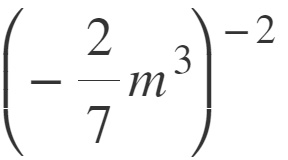
Il primo passo è quello di trasformare i numeratori in denominatori, rendendo positiva la potenza del monomio. Il segno, in questa prima fase, non va toccato!
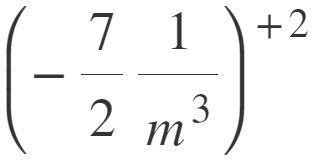
A questo punto possiamo procedere con la regola vista in questa lezione, cioè elevando al quadrato ogni singolo “pezzo” del monomio: segno, numero e parte letterale.
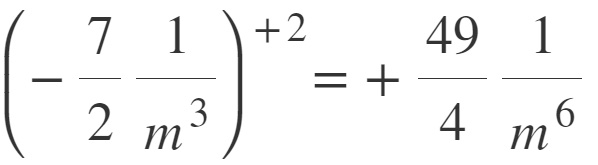
Conclusioni
Abbiamo visto in questa lezione come calcolare le potenze di monomi in maniera semplice e schematica. E’ stato visto che è sufficiente risolvere la potenza prima sul segno, poi sui coefficienti numerici ed infine sulla parte letterale.
Vuoi altri chiarimenti e suggerimenti sui monomi? Leggi subito la nostra lezione relativa alle operazioni con i monomi.