Il quadrato di un trinomio è un prodotto notevole che permette di calcolare il quadrato di polinomi composti da 3 monomi. Applicandone la regola inversa, è possibile scomporre un polinomio per ottenere un quadrato di trinomio.
Diamo per scontato, se stai leggendo questa lezione di matematica, che tu conosca come si calcola il quadrato di un binomio. La formula è praticamente la stessa, solo che bisogna tener conto che i monomi su cui effettuare il calcolo sono 3. Di seguito trovi la video lezione su come si risolvono i quadrati di trinomi, continua la lettura invece se preferisci leggerne il testo.
Quadrato di un trinomio formula
Dato un polinomio composto da 3 monomi che si sommano tra di loro A(x), B(x) e C(x) che per semplicità chiameremo soltanto A, B e C. Per calcolare il quadrato di trinomio uso la formula:
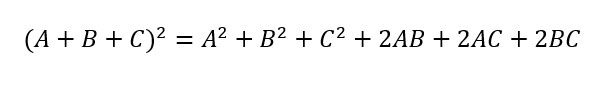
Per calcolare il trinomio al quadrato si procede nel seguente modo:
- quadrato del primo termine;
- quadrato del secondo termine;
- quadrato del terzo termine;
- doppio prodotto del primo per il secondo;
- doppio prodotto del primo per il terzo;
- doppio prodotto del secondo per il terzo.
Per evitare gli errori più comuni
Come puoi notare calcolando i quadrati di trinomi si ottengono ben 6 elementi, cioè sei monomi. Se dopo il calcolo dovessi trovarne di meno, vuol dire che hai commesso un errore. Quindi alla fine del calcolo semplicemente conta quanti monomi hai ottenuto: se sono sei vuol dire che non hai tralasciato doppi prodotti. Uno degli errori maggiori infatti è proprio quello di dimenticare di moltiplicare alcuni dei termini.
Un altro errore molto frequente è quello di dimenticare i segni. Proprio per questa ragione ti suggeriamo, soprattutto per le prime volte e fino a quando non hai sufficiente pratica, di utilizzare molto le parentesi tonde. In questo modo hai la certezza di non sbagliare. Ecco come fare.
Quadrato di un trinomio negativo – esempio
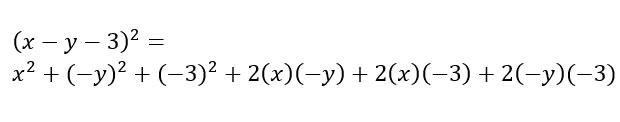
Il primo esercizio che risolviamo ha proprio dei segni meno, uno degli elementi che più causa errori e problemi agli studenti. Come puoi vedere abbiamo utilizzato sempre una parentesi tonda per riportare i vari monomi presenti nell’espressione.
![]()
In questo modo i calcoli risultano più semplici ed è praticamente impossibile sbagliare.
Dimostrazione della formula
Come si ottiene la formula del quadrato di trinomio. Semplicemente prova a moltiplicare due trinomi identici.
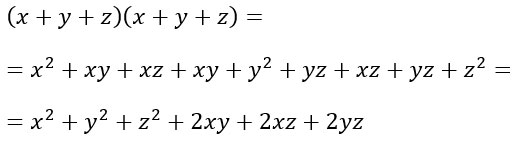
NOTA: seguendo il procedimento inverso si può ottenere la scomposizione del polinomio in quadrato di trinomio. Se cioè abbiamo i sei termini appena individuati e dobbiamo eseguire una scomposizione, sappiamo che otteniamo il trinomio al quadrato.
Esempi sul quadrato trinomio
La parte teorica è già finita. Ti consigliamo di fare attenzione con le frazioni e, come già detto, con i numeri negativi. Per il resto si tratta solo di fare un po’ di pratica. I quadrati di trinomi si risolvono con calcoli analoghi a quelli per i binomi. Facciamo qualche esempio pratico per togliere ogni dubbio.
Esercizio 1
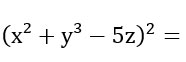
Per risolvere questo esercizio ricordate delle proprietà delle potenze, in particolare della potenza di potenza. Ricordati che in quel caso andavamo a moltiplicare gli esponenti. Ci servirà quando andremo a fare il quadrato di y alla terza. Siamo pronti a risolvere dopo questa piccola premessa.
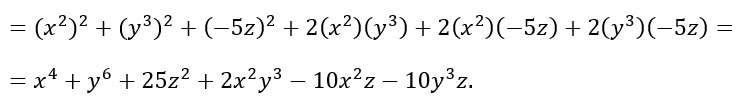
Come puoi vedere, in questo esercizio per calcolare il quadrato di un trinomio, abbiamo prima calcolato il quadrato di ogni termine, poi eseguito letteralmente il doppio prodotto di ogni singola combinazione tra i vari termini del polinomio.
Esercizio 2
Proviamo a fare un esercizio un po’ più complesso usando anche le radici, visto che sono il terrore di ogni studente. In questo caso, senza neanche ricordarci le regole dei radicali, trattiamola come se fosse una lettera.
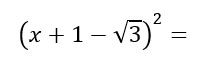
Il primo è di elevare al quadrato tutti i monomi per poi procedere con i doppi prodotti incrociati.
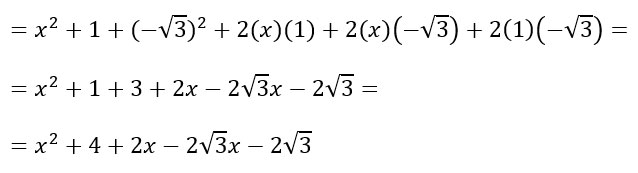
Scomposizione nel quadrato di un trinomio
Così come esiste il trinomio scomponibile nel quadrato di un binomio, anche in questo caso se siamo attenti, possiamo riconoscere un polinomio composto da 6 monomi e scomporlo in un quadrato di trinomio. Ovviamente dovranno esserci 3 termini di cui è possibile fare la radice e 3 monomi pari, di cui cioè si stata fatto il doppio prodotto. Vediamo subito un esempio pratico:
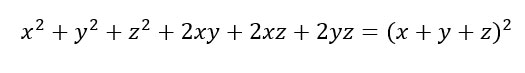
Come abbiamo fatto a capire che il polinomio si poteva scomporre nel quadrati di un trinomio?
- i primi tre elementi sono i 3 termini al quadrato;
- tutti gli altri hanno il 2 davanti, quindi possono essere considerati tutti dei doppi prodotti dei termini che prima avevamo trovato elevati al quadrato.
Il segno non lo si deduce dai termini al quadrato, visto che il quadrato rende il segno sempre positivo. Lo vediamo però dai doppi prodotti. Ad esempio 2xy ha segno positivo, per cui saranno entrambi positivi o entrambi negativi. 2xz ha invece segno negativo per cui i due monomi sono discordi: uno è positivo e l’altro è negativo. Ha senso quindi supporre che x e y siano positivi mentre z negativo.
Approfondimenti: guarda tutte le lezioni sulle scomposizioni di polinomi.
Conclusioni
Hai visto che risolvere i quadrati di trinomi è estremamente semplice una volta capita la regola generale. Imparata la formula, basta utilizzare le parantesi così da evitare di commettere errori. Se hai dei dubbi o ti piacerebbe avere ulteriori chiarimenti il nostro team è a tua disposizione.
Se invece la lezione ha risolto tutti i tuoi problemi e ti è tutto chiaro, lasciaci un commento positivo nei commenti, ci aiuterai a migliorare ogni giorno la qualità delle nostre spiegazioni.