All’interno di questa pagina vedremo alcuni dei più significativi esercizi sui prodotti notevoli. Troverai un’esercitazione completa con esempi commentati passo passo per risolvere tutti i tuoi problemi, o per far in modo che tu riesca ad affrontare anche gli esercizi più difficili.
Nel caso in cui tu non lo abbia ancora fatto, ti suggeriamo di leggere la parte teorica sui vari tipi di prodotti notevoli così da avere già a disposizione formule e strumenti di risoluzione per gli esercizi.
Prodotti notevoli, esercizi con soluzioni
In questa fase vedremo delle espressioni con prodotti notevoli da semplificare. Cerca di applicare le regole viste nella parte teorica ed evita, se possibile, di fare tutti i calcoli. In questa esercitazione cerchiamo un metodo semplice per risolvere gli esercizi. Concentrati quindi sul
Esercizio 1
Semplificare le seguenti espressioni algebriche.
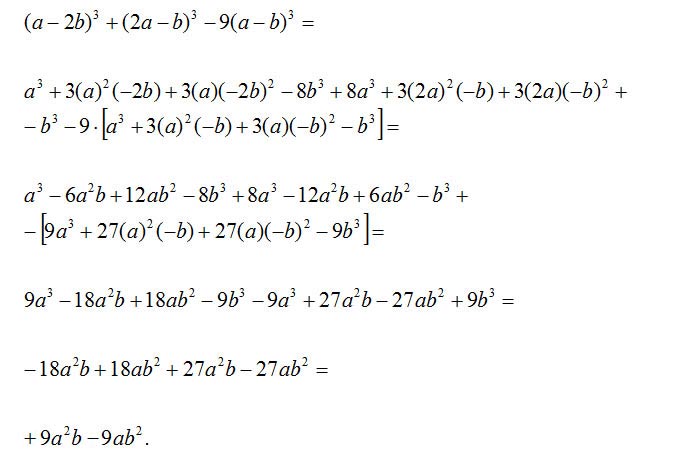
Il primo degli esercizi sui prodotti notevoli è stato svolto applicando semplicemente la regola del quadrato e del cubo di binomio. Poche somme algebriche tra monomi e il risultato si ottiene in 5 passaggi.
Esercizio svolto n.2
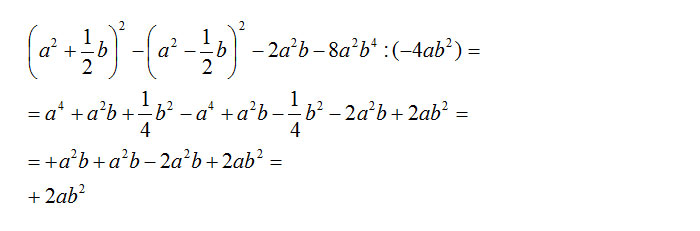
Nel secondo esempio, arrivare alla soluzione dell’esercizio sul prodotto notevole è stato molto semplice: è bastato fare il quadrato di binomio due volte, la divisione di due monomi e pochi facili passaggi algebrici.
Esercizio svolto n.3
Il prossimo esercizio è leggermente più complesso, vediamo di risolverlo assieme e di commentare il modo in cui stato risolto.
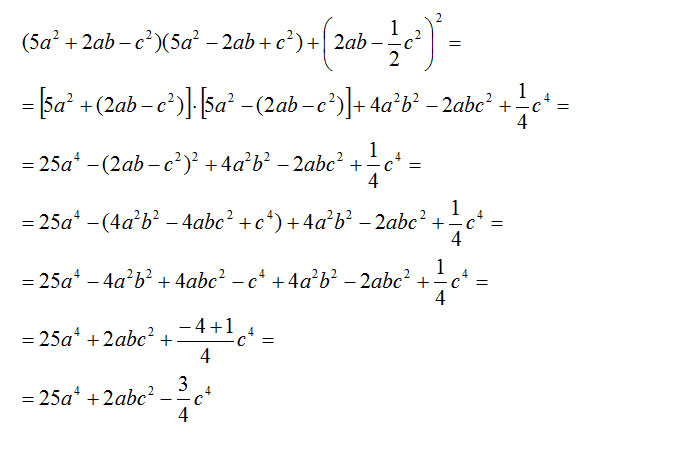
La vera difficoltà di questo esercizio sta nel riconoscere la moltiplicazione di una somma per la differenza. Negli esercizi più semplici sui prodotti notevoli siamo stati abituati a trovare quasi sempre una formula del tipo: (a+b)(a-b). In realtà è possibile trovare anche qualcosa di più complesso:

Cosa possiamo notare? Che il primo termine è lo stesso, mentre nel secondo c’è un binomio che si ripete in cui cambia solo il segno iniziale. Per cui possiamo scriverlo come:

A questo punto ci siamo ricondotti al caso precedente (a+b)(a-b) dove il primo monomio (la “a”) è in realtà un binomio e possiamo quindi risolvere con la regola dei prodotti notevoli:

Esercizio svolto n.4
Semplifica la seguente espressione nel modo più rapido possibile.
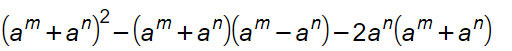
La prima tentazione dello studente è di risolvere questo esercizio sui prodotti notevoli facendo tutti i calcoli. In questo modo il problema diventa molto più difficile e lungo, con la conseguenza che è più facile sbagliare. Cerchiamo invece di osservare: c’è un elemento che si ripete sempre. a^m+a^n
Quindi il modo più veloce di arrivare alla soluzione è fare una messa in evidenza totale.
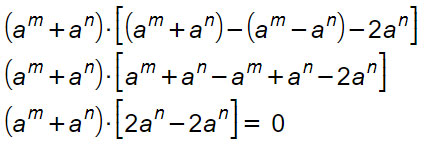
Come puoi vedere una volta eseguito il raccoglimento, bastano pochi semplici passaggi algebrici per arrivare alla soluzione.
Esercizi da risolvere
Vi alleghiamo direttamente una pagina di un testo in cui potete trovare esercizi con soluzioni sui prodotti notevoli. Ovviamente per qualsiasi dubbio o chiarimento, sia sugli esercizi che sulla teoria, il nostro staff è a tua disposizione: contattaci!

Esercizi con soluzioni sui prodotti notevoli
Nel caso tu voglia continuare ad esercitarti, a questo link troverai altri esercizi sui prodotto notevoli.
grazie molto utili
grazie a voi sono riuscita ad ottenere un bellissimo voto in matematica ( sono in prima liceo scientifico delle scienze applicate quindi non del tutte facile anzi dai miei prof è considerato un dei più difficili insieme al classico, classico europeo e linguistico) Grazie mille fino al primo trimestre sono andata abbastanza maluccio adesso con questa verifica sono riuscita a far vedere a tutta la mia classe ( che mi credevano una “perdente”) chi sono io veramente se mi impegno. grazie mille di cuore
Scusatemi, ma l’esercizio n. 500 e 503 del foglio che avete allegato potreste spiegarmi procedimenti? Grazie mille in anticipo 🙂
Per quanto riguarda l’esercizio numero 500 ti consiglio di fare un piccolo ragionamento.
Poiché x²y² può anche esser scritto come (xy)², allora fai in modo di applicare lo stesso principio alle prime due parentesi. Metti una parentesi quadra e fuori ci lasci la potenza di 2. Così puoi risolvere il prodotto della somma per la differenza e poi eventualmente fare il quadrato.
Per quanto riguarda il 503, non ci sono particolari problemi. Ci sono due quadrati di binomio e il prodotto di una somma per una differenza. Una volta risolti questi prodotti notevoli si tratta di fare qualche somma algebrica tra monomi o polinomi e si arriva presto al risultato.
Per ulteriori chiarimenti resto a disposizione.
Scusate ..ma l’ esercizio 4 e’ giusto? Nell’ultimo raccoglimento non rimane un (a^m+ a^ n ) da moltiplicare per a^n??
Correggo ultimo commento ..: da moltiplicare per 2a^n.
Ciao Stefania. Abbiamo rivisto l’esercizio n.4 e c’era un errore nella traccia. Grazie per la preziosa segnalazione, Continua a seguirci…
Grazie di cuore. In questo riesco a far esercitare mio figlio che frequenta il I liceo scientifico.
Fausto
Grazie per il tuo feedback Fausto. Cerchiamo di offrire il massimo agli studenti rendendo loro le lezioni più semplici e chiare possibili.
Continua a seguirci e buono studio per tuo figlio.