Come si trova l’area del rettangolo? Quali sono le formule da utilizzare negli esercizi? C’è solo la formula A=b·h?
In questa lezione ci occuperemo di capire come si calcola l’area di un rettangolo noti i lati, il perimetro, o la diagonale. Vedremo anche alcuni riferimenti al calcolo dell’area rettangolo inscritto in una circonferenza.
Se non hai molta confidenza con questa figura geometrica, puoi andare a leggere la lezione generale sul rettangolo così da capire quali sono le sue caratteristiche. Se invece hai bisogno di qualche approfondimento solo sulle tecniche di calcolo della superficie, allora continua la lettura.
Area rettangolo – qual è?
L’area del rettangolo è per definizione lo spazio racchiuso all’interno del perimetro.

Area rettangolo formula
Per calcolare la superficie del rettangolo è sufficiente moltiplicare base per altezza. Quindi la formula principale è:
A = b · h
Attraverso le formule inverse (b=A/h e h=A/b) è possibile calcolare base e altezza nota l’area.
Esercizi svolti
Non sempre il calcolo dell’area è così immediato. In questa seconda parte vedremo alcuni esempi svolti e commentati, partendo dagli esercizi più semplici fino ad arrivare a quelli più complessi.
Esercizio 1
Calcolare l’area del rettangolo che ha base e altezza che misurano rispettivamente 10 e 15 cm.
Svolgimento
Applichiamo semplicemente la formula Area rettangolo = base per altezza per ottenere:
A=10 cm · 15 cm = 150 cm²
Esercizio 2
Calcolare l’area del rettangolo noto il perimetro p=100 cm e la misura della base 20 cm.
Svolgimento
Avendo la misura del perimetro e della base, possiamo calcolare l’altezza attraverso la formula inversa.
p=2b+2h → 2h = p – 2h
2h = 100 cm – 2(20 cm)
h=30 cm
A questo punto possiamo calcolare la superficie con la formula usata già usata in precedente.
A = b · h
A = 30 cm · 20 cm = 600 cm²
Esercizio 3
Calcolare la misura dell’area del rettangolo nota la diagonale pari a 5 cm e la base pari a 4 cm.
Svolgimento
Per semplificarci la vita proviamo a disegnare la situazione descritta dalla traccia del problema.
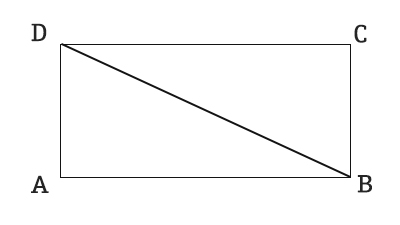
Analizziamo la figura ABD. Si tratta di un triangolo rettangolo, di cui conosciamo l’ipotenusa DB e la base AB. Con il teorema di Pitagora possiamo calcolare la misura dell’altezza DA.
AD² = DB² – AB²
AD² = (5 cm)² – (4 cm)² = 9
AD = 3 cm
A questo punto avendo base e altezza non ci resta che farne il prodotto per ottenere l’area del rettangolo.
A = b · h
A = 3 cm · 4 cm = 6 cm²
Esercizio 4
Trovare l’area di un rettangolo che ha il perimetro pari a 100 cm e la differenza di base e altezza pari a 20 cm.
Svolgimento
In questo caso abbiamo due misure, base e altezza, di cui abbiamo indirettamente la somma (cioè il semiperimetro) e la differenza. Mentre per le scuole superiori basterebbe risolvere con le equazioni di primo grado, alle scuole medie dobbiamo fare diversamente.
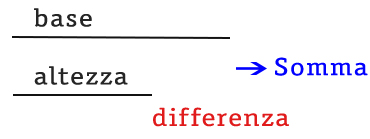
Abbiamo quindi somma e differenza di due segmenti. Quello più piccolo, che abbiamo considerato l’altezza, può essere calcolato come somma meno differenza diviso due.
p/2= somma = s = 100:2 = 50 cm
differenza = d = 30 cm
h = ( s – d ) :2
h = (50 cm – 20 cm) : 2 = 15 cm
A questo punto l’altro segmento è pari a:
b = h+d = 15 + 20 = 35 cm
Per il calcolo dell’area del rettangolo, come prima, basta ora moltiplicare base per altezza:
A = b · h = 35 cm · 15 cm = 525 cm