Una guida semplice e completa per risolvere le equazioni binomie di grado superiore al secondo. Un riferimento speciale alle equazioni biquadratiche con consigli, trucchi ed esercizi svolti.
Equazioni binomie
Equazioni biquadratiche
Esercizi sulle equazioni di grado superiore al secondo
Prima di vedere cosa sono le equazioni binomie, facciamo il punto della situazione. Quando cerchiamo di risolvere un’equazione, la prima cosa che andiamo ad analizzare è il grado del polinomio, cioè l’esponente massimo della nostra equazione. Con una semplice occhiata possiamo capire che tipo di esercizio dobbiamo risolvere.
Se infatti il grado è 1 abbiamo un’equazione di primo grado lineare, se il grado è 2 abbiamo invece esercizi sulle equazioni di secondo grado… e se il grado è maggiore di 2? A quel punto può venire in nostro soccorso solo la regola di Ruffini.
Ma ci sono alcuni casi particolari in cui possiamo risolvere funzioni che sembrano difficili in maniera molto semplice. Stiamo parlando dello svolgimento delle funzioni quadratiche. Vediamo più nel dettaglio di cosa stiamo parlando.
Equazioni binomie
Le equazioni binomie sono sono equazioni composte da un binomio, cioè da due monomi. Possiamo trovarci ad affrontare equazioni binomie di secondo grado. Siamo nel caso delle equazioni pure e spurie che abbiamo già visto nelle precedenti lezioni.
Il caso più difficile però, che mette in difficoltà molti studenti, riguarda le equazioni di grado superiore al secondo. In realtà, così come per le equazioni biquadratiche o trinomie, gli esercizi sulle equazioni binomie sono molto facili da risolvere:
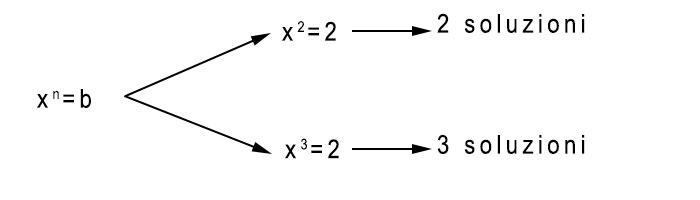
Nell’esempio di equazione binomia puoi vedere come ci siano due casi principali: esponente pari ed esponente dispari. In entrambi i casi sarà sufficiente semplicemente portare il termine noto al secondo membro e poi fare la radice ennesima.
Il trucco che ti consigliamo di ricordare è che se il numero dell’esponente rappresenta anche il numero di soluzioni possibili. Quindi se ho un’equazione binomia di grado 5, ho cinque soluzioni. La differenza tra esponente pari e dispari è che nei pari devo ricordarmi di mettere un + e – davanti la soluzione. In caso di esercizio con equazione binomia ad esponente dispari le n soluzioni saranno tutte uguali. Vediamo un esempio concreto.

Equazioni biquadratiche
Le equazioni biquadratiche non sono altro che equazioni riconducibili al II grado. Gli esercizi sulle biquadratiche sono molto semplici da risolvere: è sufficiente porre l’incognita al quadrato pari ad una nuova lettera temporaneamente e risolvere l’equazione di II grado che ne risulta. Puoi usare sia la formula ridotta che la normale. Noi optiamo per la seconda.
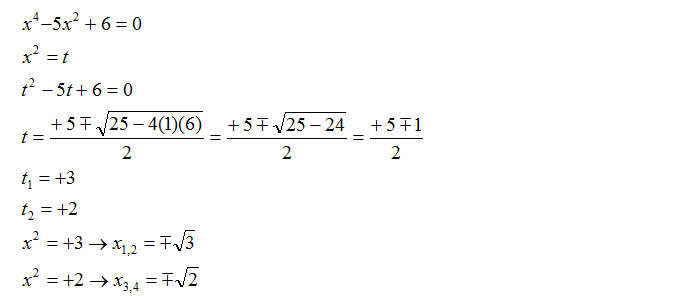
Come puoi vedere nell’esempio, è importante poi sostituire per la seconda volta la variabile t assegnata riconducendoci al caso degli esercizi sulle equazioni binomie. L’esercizio svolto mostra chiaramente inoltre che il risultato mi porta a quattro diverse soluzioni. Questo perché il grado del polinomio corrisponde al numero di soluzioni.
Equazioni di grado superiore al secondo esercizi
Il primo che vi proponiamo è un esercizio svolto sulle equazioni biquadratiche. Si risolve così come abbiamo visto nell’esempio precedente.
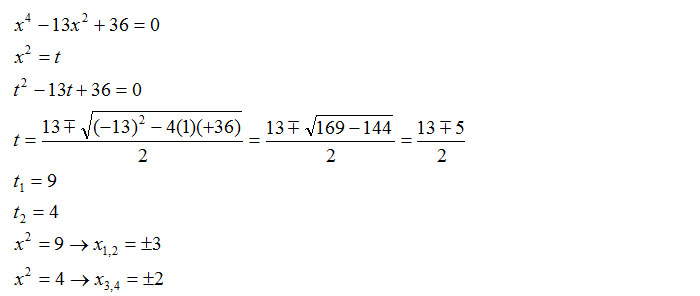
Quello che possiamo risolvere ora è un’ulteriore esercizio sulle equazioni biquadratiche, con la differenza questa volta che abbiamo una potenza sesta. La sostituzione è leggermente diversa. Vediamo subito come risolverlo in maniera semplice:
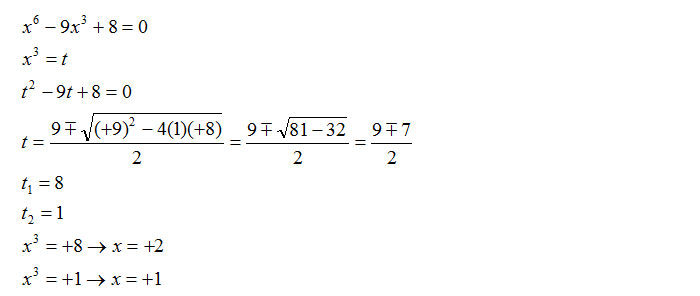
Per ulteriori esercizi sulle equazioni binomie, biquadratiche e trinomie puoi andare alla pagina puoi cercare di risolvere le seguenti tracce. Per dubbi, chiarimenti e un aiuto sugli esercizi, non esitare a contattarci, il nostro staff sarà felice di risponderti.