In questa lezione vedremo come si risolvono le equazioni di primo grado, vedremo una spiegazione completa con le regole da utilizzare e alcuni esercizi svolti per facilitarne l’apprendimento.
Se i concetti teorici ti sono già chiari e vuoi passare direttamente alla parte pratica dell’esercitazione, vai agli esercizi sulle equazioni di primo grado.
Equazioni di primo grado definizione
Si definiscono equazioni di primo grado quelle uguaglianze tra due espressioni algebriche in cui compare almeno una volta l’incognita x elevata alla potenza 1.
Si tratta cioè di un’uguaglianza di due polinomi a destra e sinistra dell’uguale in cui compare l’incognita x.
Polinomio a sinistra = Polinomio a destra
Matematicamente possiamo indicare un’equazione di primo grado come:
P(x) = Q(x)
dove P(x) e Q(x) sono due polinomi di primo grado.
Le equazioni di primo grado vengono chiamate anche equazioni lineari perché, come studierai nel programma di geometria analitica, l’equazione della retta nel piano cartesiano è proprio definita da un’equazione di primo grado.
Esempio:
![]()
In questo caso P(x)=2x+1, mentre Q(x)=0. Per trovare il risultato delle equazioni di primo grado occorre trovare quella che viene definita soluzione dell’equazione. Serve cioè quel valore che, assegnato all’incognita x, soddisfa l’uguaglianza.
Nell’equazione di primo grado in alto se provi a mettere al posto della x il numero -1/2, vedrai che il risultato che ottieni è 0=0, per cui x=-1/2 è la soluzione dell’equazione.
Vedremo tra un istante come si calcolano le soluzioni delle equazioni di primo grado.
I membri dell’equazione
Come puoi notare negli esempi in alto, la caratteristica delle equazioni di primo grado è di avere un “uguale” che divide due membri.
- tutto ciò che è a sinistra dell’uguale si chiama primo membro;
- tutto ciò che è a destra dell’uguale si chiama secondo membro.
Come risolvere le equazioni di primo grado
Non importa quanto l’espressione sia difficile o lunga, l’obiettivo è sempre ricondursi alla forma normale:

Per arrivare a questo punto, bisogna fare tutte le operazioni classiche dell’algebra (somme, prodotti, …) . Alla fine sono soltanto due le regole che bisogna sapere per poter risolvere le equazioni lineari:
- Principio di Addizione e Sottrazione: aggiungendo o sottraendo una stessa quantità ad entrambi i membri dell’equazione il risultato non cambia.
- Principio di Moltiplicazione e Divisione: Moltiplicando o dividendo entrambi i membri dell’equazione per una stessa quantità il risultato non cambia.
Facciamo un esempio pratico per capire quali conseguenze hanno queste due regole nello svolgimento delle equazioni di primo grado.
Esempio:
2x+1=0
Per arrivare alla forma normale bisogna isolare al primo membro tutti i termini con la x, mentre i termini noti (si chiamano così tutti i termini non contenenti l’incognita) vanno spostati al secondo membro. Per far ciò applico la prima regola, cioè sottraggo 2 ad entrambi i membri.
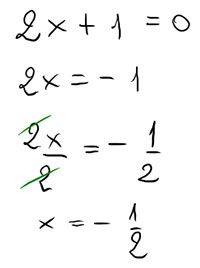
OSSERVAZIONE → la prima regola può essere sintetizzata come segue: per spostare un monomio da un membro all’altro di un’equazione di primo grado basta cambiargli il segno. Infatti il +1 che era al primo membro nella traccia è diventato -1 nell’ultimo passaggio.
Proviamo con un esempio un po’ più complicato.
![]()
In questo caso abbiamo una parentesi tonda e delle semplici moltiplicazioni da svolgere.
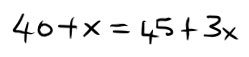
A questo punto teniamo tutti gli elementi con la x a sinistra e tutti i termini noti a destra, cambiando i segni dove necessario.
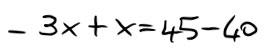
Possiamo ora svolgere le somme algebriche a primo e secondo membro.
![]()
Applichiamo infine il principio di moltiplicazione e divisione per spostare il 2 al secondo membro.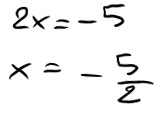
Equazioni di primo grado con frazioni
Abbiamo visto fino ad ora che anche per risolvere le equazioni di primo grado difficili basta semplicemente fare delle operazioni tra monomi fino ad arrivare alla forma normale. La cosa si complica leggermente quando ci sono delle frazioni. In questo caso bisogna calcolare il minimo comune multiplo.
ATTENZIONE: nella frazione non può comparire l’incognita x, altrimenti ci troveremmo di fronte ad un’equazione di primo grado fratta.
Per risolvere le equazioni con le frazioni, come detto, bisogna calcolare il m.c.m. così da creare un denominatore unico che poi può essere eliminato. Vediamo un esempio pratico:
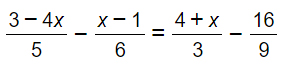
Svolgimento:
Come puoi vedere dalla traccia, si tratta di un’equazione di primo grado con le frazioni. Il primo passo è quindi quello di calcolare il minimo comune multiplo.
mcm = 3²·2·5 = 90
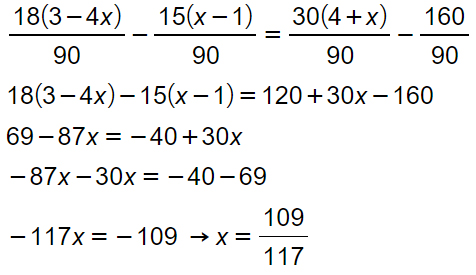
Equazioni di primo grado a coefficienti irrazionali
Gli studenti in genere trovano maggiori difficoltà quando ci sono equazioni di primo grado con le radici. Il problema non è nella risoluzione dell’equazione, ma nella gestione dei radicali e nelle varie operazioni da portare avanti. Ovviamente per evitare di commettere errori è importante conoscere bene le regole e le proprietà dei radicali.
Proviamo a fare un esempio pratico:
√3 x = √6 + √27
Poiché l’obiettivo è riportarci nella forma canonica delle equazioni di I grado, cioè ax=b. In questo caso la traccia ha già portato tutti i termini noti al secondo membro. Bisogna però dividere entrambi i membri per radical 3 per tenere l’incognita x da sola.
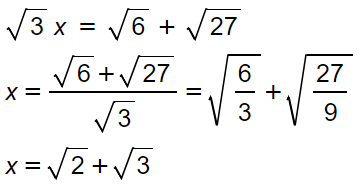
Problemi riconducibili a equazioni di primo grado
Le equazioni di primo grado sono uno strumento utile anche nella vita reale per risolvere problemi concreti. Non ci credi? Prova a vedere come abbiamo risolto questi problemi con le equazioni di primo grado.
Problema con le equazioni
In un cortile ci sono polli e conigli: in totale ci sono 40 teste e 130 zampe. Quanti sono i polli e quanti i conigli?
Svolgimento
Avrai tante difficoltà a risolvere questo problema a mente. Vediamo di risolverlo matematicamente. Cosa sappiamo?
- totale teste: t=40
- totale zampe: z=130
- 1 pollo ha 1 testa e 2 zampe
- 1 coniglio ha 1 testa e 4 zampe
Incognite:
numero di polli: x=?
numero di conigli: y =?
Quindi x+y=40, da cui y=40-x (è il numero di conigli). Le zampe dei polli sono 2x, le zampe dei conigli sono 4y, quindi 4(40-x), poiché la loro somma è 130, posso scrivere:
2x+4(40-x)=130
2x+160-4x=130
-2x=130-160
2x=30
x=15
y= 40-x =25
Ci sono quindi 15 polli e 25 conigli.
Conclusioni
In questa lezione abbiamo visto come risolvere le equazioni di primo grado, qualsiasi sia il livello di difficoltà. Abbiamo visto come comportarci con le frazioni e anche in presenza di radicali. A questo punto sei pronto per esercitarti.
Vai subito agli esercizi sulle equazioni di primo grado.
Se questa pagina ti è stata d’aiuto nella comprensione dei tuoi esercizi o ti ha aiutato a far chiarezza con i concetti appresi a scuola, lascia un commento positivo in basso. Se dovessi aver ulteriore domande, sentiti libero di inoltrarcele tramite i commenti in basso. Saremo felici di aiutarti nel minor tempo possibile.
Molto lineare e ben esposta la spiegazione. Complimenti
Grazie 1000 davvero grazie
Dopo aver letto questa spiegazione finalmente ho capito le equazioni,grazie per aver fatto questo sito.
Domani ho il compito in classe sulle equazioni.. speriamo bene!!
ottima spiegazione, grazie
3x+2x-5=4x+3x-2x
Usando la regola dell’addizione e sottrazione, sposto tutte le incognite a sinistra e i termini noti a destra. Nello spostamento ricordiamoci di cambiare i segni.
3x+2x+2x-4x=+3+5
Non ho capito, se devo spostare tutte le incognie a sinistra perchè 3x di destra rimanare sulla destra e perda la x ?
Devo ristudiare per aiutare mia figlia, no ricordo assolutamente nulla.
Grazie
Ciao Miria,
c’era un errore nella traccia che abbiamo subito provveduto a correggere. Grazie per la segnalazione.
Riprova ora a risolvere e se hai bisogno non esitare a chiedere 😉
Veramente spiegato in modo semplice.Imposaibilw non capire matematica spiegata così bene!!!