Il teorema di Talete è un teorema della geometria piana che mette in relazione i segmenti che si formano su due generiche traversali tagliate da un fascio di rette parallele. In questa lezione vedremo la sua definizione, o meglio il suo enunciato, ma soprattutto ci concentreremo sulla parte pratica. Cioè come si applica il teorema di Talete sui triangoli?
Teorema di Talete – enunciato
Se un fascio di rette parallele è tagliato da due trasversali, i segmenti determinati su una trasversale sono proporzionali ai corrispondenti segmenti dell’altra trasversale.
Ad una prima lettura il teorema di Talete può sembrare difficile ed è forse questa la ragione per cui molti studenti ne sottovalutano l’importanza. Proviamo a spiegare in maniera più semplice la definizione, magari facendo riferimento ad una figura.
Per comprendere meglio il teorema di Talete iniziamo disegnando un fascio di rette parallele, ciascuna delle quali viene indicata in figura da una lettera minuscola (a, b, c, …) A questo punto si disegnino due trasversali r e r’. Queste intersecano il fascio in punti che chiameremo A, A’, B, B’, …
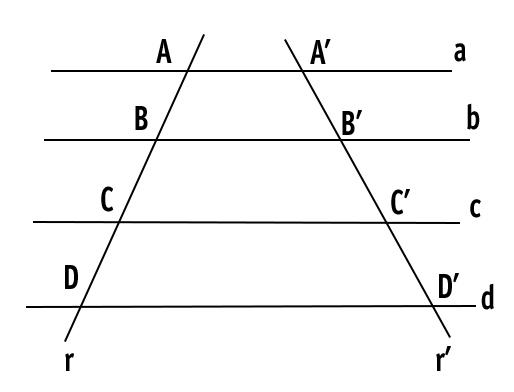
Si dicono corrispondenti quei segmenti sulle trasversali che sono compresi tra le stesse parallele. Ad esempio AB è corrispondente ad A’B’, così come BC e corrispondente a B’C’, eccetera. Dobbiamo cioè dimostrare la loro proporzionalità, per cui:
AB:A’B’=AC:A’C’=CD:C’D’=…
Come puoi notare abbiamo considerato anche i “segmenti somma” come AC e A’C’. Inizia ad esserti più chiaro ora l’enunciato del teorema di Talete? Date due parallele tagliate da due trasversali, i segmenti corrispondenti che si formano sono tra loro proporzionali.
Dimostrazione del Teorema di Talete
Generalmente non viene chiesta agli studenti delle scuole medie, ma al biennio delle superiori può essere una possibile domanda di interrogazione. Esistono tante dimostrazioni del Teorema di Talete, noi ti illustriamo quella che abbiamo ritenuto la più semplice e che abbiamo studiato quando eravamo a scuola. Non farti spaventare dalla lunghezza della dimostrazione, è solo trovi spiegati tutti i vari passaggi così da semplificarti al massimo la comprensione.
Iniziamo ricordando il primo criterio di proporzionalità: condizione necessaria e sufficiente affinché le grandezze di due classi in corrispondenza biunivoca siano direttamente proporzionali è che:
- a grandezze uguali di una classe corrispondano grandezze uguali dall’altra classe;
- alla somma di due più grandezze qualsiasi di una classe corrisponda la somma delle grandezze corrispondenti dell’altra classe;
Detto in parole povere: considerando che tra i segmenti corrispondenti c’è una corrispondenza biunivoca, per dimostrare il teorema di Talete dobbiamo fare due cose:
- dimostrare che a segmenti uguali di r corrispondono segmenti uguali di r’;
- alla somma di due segmenti di r corrisponde la somma dei corrispondenti segmenti di r’.
Prima parte
Affrontiamo la prima parte del teorema di Talete, cioè dobbiamo dimostrare che se ci sono segmenti uguali su r, allora i segmenti corrispondenti su r’ sono a loro volta uguali.
Per dimostrare questa condizione ci viene in aiuto un teorema della geometria per cui se un fascio di rette parallele è tagliato da due trasversali, a segmenti uguali dell’una corrispondono segmenti uguali dell’altra. In buona sostanza questo teorema già soddisfa la nostra richiesta e risponde alla domanda di questa prima parte di dimostrazione del Teorema di Talete.
Seconda parte
Per quanto riguarda la seconda condizione, occorre provare ad esempio che alla somma AB+BC corrisponde la somma A’B’+B’C’. Ciò è verificato in quanto ad AC, somma dei segmenti AB e BC, corrisponde proprio A’C’ che è il segmento somma di A’B’ e B’C’. In questo modo abbiamo quindi dimostrato il Teorema di Talete.
Corollari ed applicazioni sui triangoli
Come abbiamo detto ad inizio lezione, il teorema di Talete può essere applicato in numerosi problemi di geometria in cui ci sono i triangoli.
Corollario
Una retta parallela ad un lato di un triangolo determina sulle rette degli altri due lati segmenti proporzionali.
Dato un triangolo ABC come nella figura che segue, siano P e Q i punti in cui una parallela al lato BC interseca le rette AB e AC.
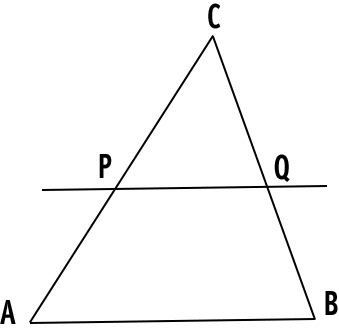
Vogliamo dimostrare che:
AB:AC=AP:AQ=PB:QC
Infatti condotta per A la retta MN parallela a BC, si perviene alla tesa applicando il teorema di Talete alle parallele PQ e BC tagliate dalle trasversali AB e AC. Vale ovviamente anche l’inverso del corollario visto sopra. Cioè una retta che determina sulle rette di due lati di un triangolo segmenti proporzionali, è parallela al terzo lato.