Come si trova il perimetro del rombo? Quali sono le formule da utilizzare negli esercizi? In questa lezione vedremo alcuni esempi ed esercizi svolti che ci aiuteranno a capire in maniera semplice come si calcola il perimetro di un rombo in base ai dati a disposizione.
Formula perimetro rombo
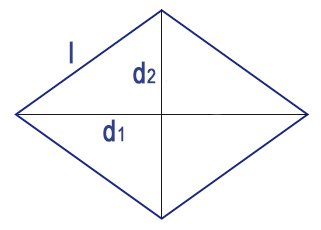
Il perimetro del rombo rappresenta la somma dei lati della figura geometrica. Essendo i lati tutti uguali, per calcolare il perimetro di un rombo è sufficiente conoscere la misura di un lato e moltiplicarlo per 4.
![]()
Dove l è la misura del lato, d1 e d2 le misure delle diagonali e p il perimetro del rombo.
Approfondimenti: tutte le formule sul rombo – il formulario completo
Esercizio 1
Il lato di un rombo misura 20 cm. Calcolare il perimetro.
Svolgimento
Il primo problema affrontato non comporta particolari difficoltà. Avendo il lato, si ottiene il perimetro del rombo moltiplicandolo per 4. Per cui:
P= 4l = 4·20 cm = 80 cm
Come calcolare il perimetro del rombo note le diagonali
Non sempre si è così fortunati di avere subito dalla traccia il lato della figura. Può capitare che vengano date più o meno direttamente le misure delle diagonali.
In tal caso si può considerare uno dei 4 triangoli rettangoli che vengono formati dalle diagonali e, considerando le semi-diagonali del rombo come i cateti, si può ricavare il lato come ipotenusa con il teorema di Pitagora. Vediamo subito come fare…
Esercizio 2
La diagonale maggiore di un rombo misura 20 cm e la minore è i suoi 3/4. Calcola il perimetro e l’area del rombo.
Svolgimento
Non c’è bisogno di fare neanche il disegno perché la traccia ci fornisce indirettamente la misura delle due diagonali. Sappiamo che la minore è 3/4 rispetto alla maggiore. Matematicamente possiamo scrivere che:
d2= d1 · 3/4 = 20 cm · 3/4 = 15 cm
Calcoliamo a questo punto le semidiagonali considerandole cateti del triangolo AOD.
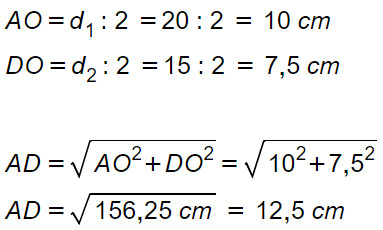
Una volta calcolato il lato, si può trovare il perimetro del rombo moltiplicando il lato per 4. Per cui:
P= 4l = 4·12,5 cm = 50 cm
Lasciamo al nostro lettore il calcolo dell’area. Avendo le diagonali basta applicare la formula e si arriva in un istante alla soluzione.
Esercizio 3
La somma delle diagonali di un rombo misura 98 cm e una è 3/4 dell’altra. Calcola il perimetro del rombo.
Svolgimento
Gli studenti delle scuole superiori possono imporre la diagonale maggiore pari a x e scrivere un’equazione di primo grado x+3/4x=98 cm.
Gli studenti delle scuole medie invece possono ragionare per unità frazionarie. La diagonale maggiore è 4 unità mentre la minore è 3 unità.
Vuol dire che in totale ci sono:
d1+d2 = 4u+3u = 7u = 98 cm
1u=98cm/7 = 14 cm
d1=4u = 14·4= 56 cm
d2=3u = 14·3= 42 cm
A questo punto siamo tornati al caso precedente. Abbiamo le due diagonali e serve il perimetro del rombo. Si calcolano così le semidiagonali, teorema di Pitagora per ottenere il lato e infine si moltiplica per 4.
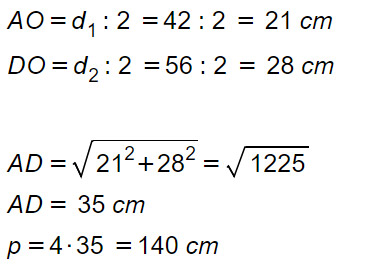
Conclusioni
Abbiamo visto in questa lezione che esiste una sola formula per calcolare il perimetro di un rombo. Una volta calcolato il lato, è sufficiente moltiplicarlo per 4.
Se questa lezione ti è stata d’aiuto o se hai ulteriori dubbi, non esitare a lasciare un messaggio nei commenti. Il nostro staff ti risponderà nel minor tempo possibile.