Come si calcola il perimetro di un quadrato? Quante formule ci sono che possono essere utilizzate negli esercizi? E’ possibile calcolare il perimetro del quadrato conoscendo l’area? In questa lezione risponderemo a tutte queste domande analizzando non solo le formule, ma anche vedendo alcuni esercizi ed esempi svolti.
Nella lezione generale sul quadrato, abbiano analizzato tutte le formule che riguardano questa semplice figura geometrica. Abbiamo detto che, trattandosi di un poligono regolare, tutte le formule si semplificano. Per cui anche il perimetro del quadrato, piuttosto che essere calcolato facendo la somma dei lati, si può calcolare con una formula ridotta.
P=4·l
Poiché ci sono 4 lati congruenti, allora la formula del perimetro del quadrato è lato per quattro. Cioè basta avere la misura di uno qualsiasi dei lati, moltiplicarla per 4 per ottenere la misura del perimetro, cioè l’estensione del contorno della figura geometrica.
Formule perimetro quadrato
Di seguito sono elencate le tre formule da usare nei problemi a seconda che ci sia a disposizione l’area del quadrato, la misura del lato o della diagonale del quadrato.
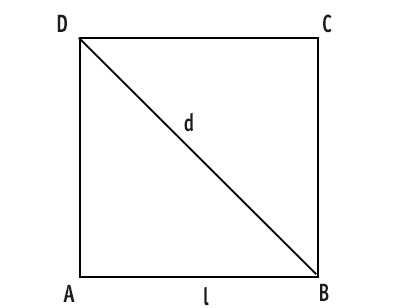
P= 4·l = 4·AB
Perimetro quadrato conoscendo i lati
p=4·√A
Perimetro quadrato conoscendo l’area
p= 2√2·d = 2·√2DB
Perimetro quadrato conoscendo la diagonale
Poiché nel programma di geometria si alle scuole medie che superiori certamente non mancheranno le formule, non ha senso aggiungerne altre inutili. Per questa ragione ti consigliamo di imparare solo la prima a memoria. Le altre o le ricavi oppure fai un passaggio in più come stai per vedere negli esercizi svolti.
Esercizi sul perimetro del quadrato
Problema 1
Calcolare il perimetro di un quadrato che l’area pari a 196 cm².
Svolgimento
Per evitare di imparare a memoria le cose superflue, calcoliamo l’incognita del problema usando solo la formula P=4L. Poiché abbiamo l’area, con la formula inversa possiamo ricavare il lato.
A=l² → l=√A
l=√(196 cm² )=14 cm
A questo punto applico la formula per calcolare il perimetro di un quadrato noto il lato:
P=4·l = 4·(14cm) = 56 cm
Problema 2
Calcolare il perimetro di un quadrato la cui diagonale misura 20 mm.
Svolgimento
Il procedimento è analogo al precedente ma questa volta abbiamo a disposizione la diagonale. Per cui, ricorrendo alla sua formula inversa, abbiamo:
d= l√2 → l = (√2)/2 · d
l= 20√2 mm
A questo punto, avendo la misura del lato, possiamo calcolare il perimetro del quadrato:
p= 4 L = 4(20√2 mm) = 80√2 mm ≅ 113,14 mm