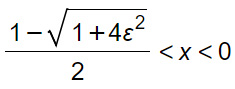Limite destro e sinistro di una funzione

Il calcolo del limite destro e sinistro di una funzione si rende necessario qualora si voglia studiare il comportamento di una curva nell’intorno destro o sinistro di un suo punto.

In particolare il limite sinistro è un limite in cui i valori tendono da sinistra al punto x₀. Il limite destro è un limite in cui i valori tendono da destra al punto x₀.

Vediamo però di essere più chiari e di spiegare in maniera più semplice ma precisa cosa sono il limite destro e sinistro di una funzione.

Cosa sono il limite destro e sinistro?

Capiterà più volte di dover studiare il comportamento di una funzione nell’intorno di un punto x₀, detto punto di accumulazione. Può essere interessante capire cosa succede un po’ prima o un po’ dopo che la x raggiunga questo punto.

Per questa ragione si studiano il limite destro o sinistra, a seconda che ci si concentri sull’intorno destro o sinistro del punto x₀.

Detto in maniera più semplice: se stiamo studiando una curva, a quale valore tende la y, se la x tende

• da sinistra a x₀, cioè ha dei valori che aumentano sempre più fino ad arrivare a x₀? (LIMITE SINISTRO)
• da destra a x₀, cioè ha dei valori che diminuiscono sempre più fino ad arrivare a x₀? (LIMITE DESTRO)

Vedremo anche degli esempi in basso in cui studieremo proprio il comportamento di una funzione analizzandone limite destro e sinistro. Prima vediamo le definizioni…

Definizione di limite destro e sinistro

Limite destro

Data una funzione reale y=f(x) con un punto di accumulazione x₀, diremo che il valore l è il limite destro della funzione f(x) e si scrive come:

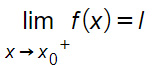
se, fissato un valore ε positivo piccolo a piacere, esiste un δ positivo funzione di ε , che rispetta la condizione x₀< x< x₀+δ e risulta |f(x)-l|<ε. Per cui possiamo scrivere.

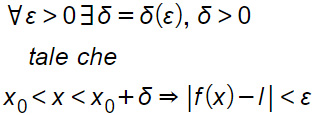
Suggerimenti utili

• Da notare come scrivere x₀< x< x₀+δ faccia proprio riferimento all’intorno destro di x₀.
• Non confondere il limite destro e sinistro di una funzione. Il destro in questo caso ha vicino il punto di accumulazione il simbolo + (più).

Limite sinistro

Data una funzione reale f(x), con un punto di accumulazione x₀ appartenente al dominio della funzione, diciamo che essa tende a l da sinistra e scriviamo:

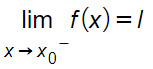
se fissato un se, fissato un valore ε positivo piccolo a piacere, esiste un δ positivo funzione di ε , che rispetta la condizione x₀-δ< x< x₀ e risulta |f(x)-l|<ε. Per cui possiamo scrivere.

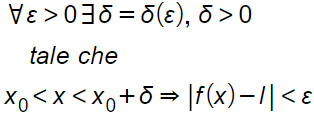
Suggerimenti utili

• In questo caso l’intorno sinistro è rappresentato da  x₀-δ< x< x₀ .
• Per distinguere il limite destro e sinistro, in questo caso si usa il simbolo – (meno) accanto al punto di accumulazione.

Limite destro e sinistro infinito

Le definizioni che abbiamo analizzato nei casi precedenti riguardano il caso di limite finito che tende a un valore finito.

Sappiamo che esistono altre tre casi da prendere in considerazione. Puoi trovare i casi generali nella lezione sulla definizione di limite. Per arrivare ai casi con i limiti infiniti basterà fare dei piccoli aggiustamenti e considerare, per il limite destro e sinistro, rispettivamente l’intorno destro e sinistro di x₀.

Calcolo limite destro e sinistro esercizi svolti

Eseguire il calcolo del limite destro e sinistro, tenendo presente le definizioni viste sopra.

Esercizio svolto 1

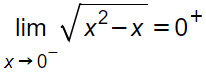
Svolgimento

Siamo nel caso di limite finito per x tendente a valore finito da sinistra. Come facciamo a dirlo? Dal segno – (meno) che compare sul punto di accumulazione.

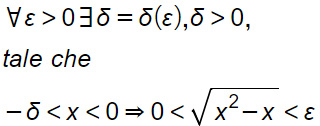
Analizziamo l’ultima diseguaglianza. Questa equivale ad un sistema di disequazioni di primo grado. Questo perché le diseguaglianze devono essere verificate contemporaneamente.

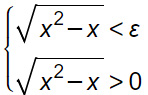
Una volta impostato il sistema e scritte le condizioni di esistenza delle disequazioni irrazionali, passiamo al loro svolgimento.

La seconda è sempre verificata a patto che siano rispettate le condizioni di esistenza, cioè per x∈(-∞;0] U [+1;+∞)

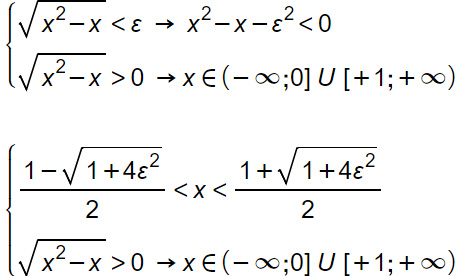
La soluzione del sistema che verifica la definizione è: