In questa lezione introduciamo la definizione di limite di una funzione, andandone a studiare quella che viene chiamata definizione rigorosa – abbastanza ostica per molti studenti – cercando di semplificarla e renderla il più chiara possibile.
Il concetto di limite ha un’importanza fondamentale nel programma di analisi infinitesimale. Cerchiamo di avvicinarci alla definizione rigorosa di limite facendo alcuni piccoli ragionamenti.
Cosa sono i limiti?
Sia data l’equazione della retta y=2x+3. Studiamo il comportamento della variabile y quando x “si avvicina” al valore 2.
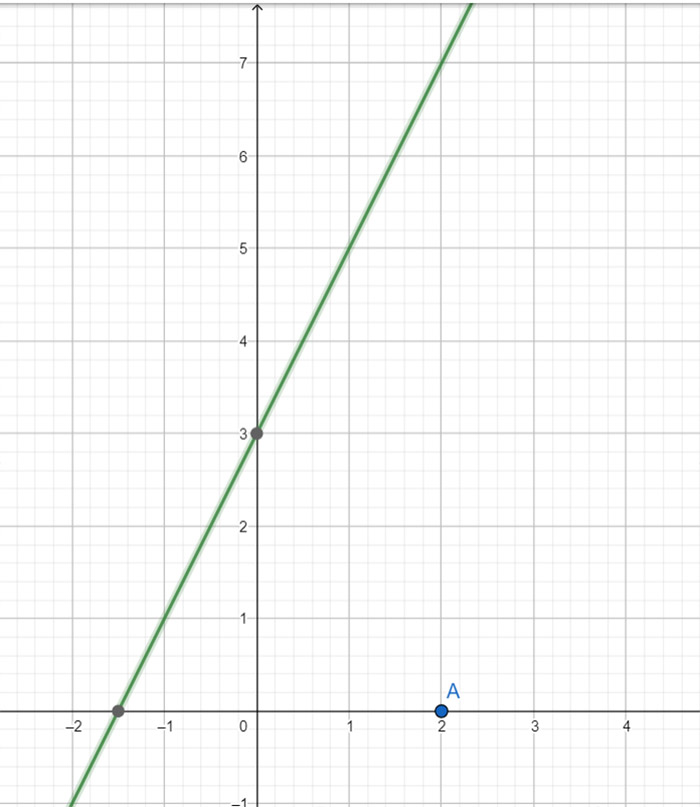
Creiamo una tabella in cui attribuiamo ad x valori che si avvicinano sempre più a 2.

Si nota che man mano che ci avviciniamo alla x=2, la y tende (cioè si avvicina) sempre più al valore 7.
Questo vuol dire che la differenza in valore assoluto – perché non ci interessa il segno – tra 7 e il valore di y trovato nella tabella, quando x si avvicina molto a 2, diventa davvero piccolissimo.
Ad esempio quando x=2,001, y=7,002. Allora la differenza |7-7,002|=0,002, è cioè un numero piccolo a piacere.
In simboli scriviamo che:
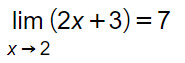
Si lette “limite per x tendente a 2 di 2x+3 uguale a 7“.
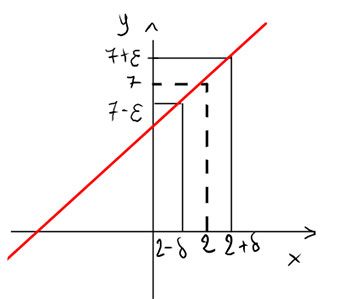
Definizione di limite finito
Limite finito di una funzione per x tendente ad un valore finito.
Diciamo che f(x) ha limite l per x tendente a x0 e scriviamo:
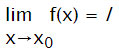
per ogni numero positivo ε è possibile determinare un numero positivo δ, in generale funzione di ε, tale che per ogni x appartenente al dominio di f(x), con x≠x0, e tale che
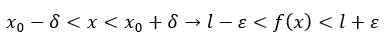
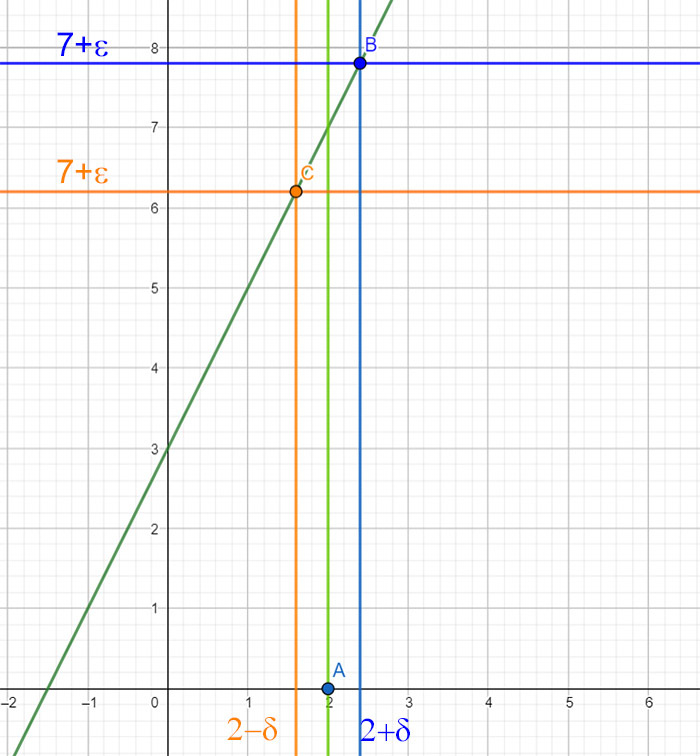
La scrittura appena esposta somiglia la possiamo riscontrare proprio nel grafico visto poco fa in alto, dove x0=2 e l=7. Si nota che sull’asse delle x ci troviamo in un intervallo compreso tra (x0-δ) e (x0+δ), mentre sull’asse delle y ci troviamo in un intervallo compreso tra (l-ε) e (l+ε).
In linguaggio matematico formale, volendo esprimere la definizione di limite matematica, possiamo anche scrivere:
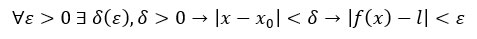
Che vuol dire?
Dividiamo la definizione in pezzi così da rendere tutto più chiaro.
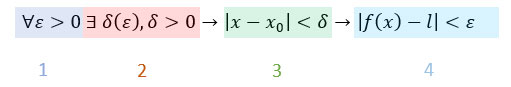
- Per ogni ε positivo, piccolo a piacere;
- Esiste un δ positivo piccolo a piacere, il cui valore dipende da ε (c’è scritto infatti δ=δ(ε));
- Tale che la differenza in valore assoluto tra la x e x0 è minore di δ – cioè i valori di x e x0 sono così vicini che la loro differenza è infinitesima
- Tale che la differenza in valore assoluto tra f(x) e l è minore di ε – cioè i valori di f(x) e l sono così vicini che la loro differenza è infinitesima.
Esempio
Verifichiamo che il limite per x che tende a 0 di (x^2+2) è uguale a 2
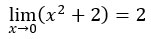
In questo caso abbiamo che x0=0 e l=2. Preso un generico numero piccolo a piacere e positivo, ε>0, dobbiamo determinare ora δ in funzione di ε, cioè δ=δ(ε), tale che x0-δ<x<x0+δ, tale che |f(x)-2|<ε.
Sostituiamo la funzione x^2+2 al posto di f(x):
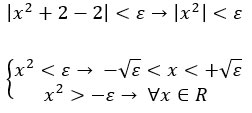
Quindi δ è uguale alla radice di ε
Definizione di limite infinito per x tendente a un valore finito
Diciamo che f(x) ha per limite +∞ per x tendente a x0, e scriviamo:
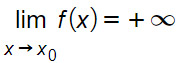
preso a piacere un numero M>0 esiste in corrispondenza un δ>0, tale che preso x appartenente al dominio della funzione f(x), diverso da x0, e tale che:
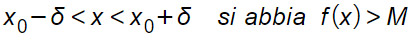
Possiamo scrivere la definizione di limite infinito anche in linguaggio formale.
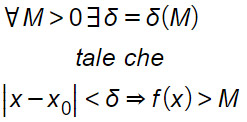
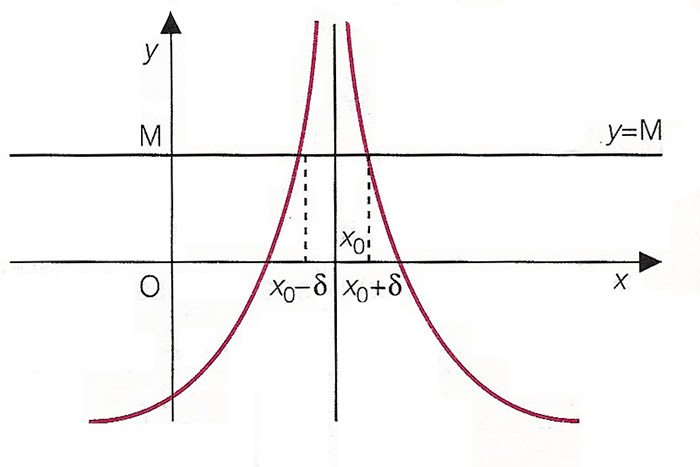
Dal grafico si può dedurre il concetto di limite infinito. Dato un valore M generico (non importa quanto grande), i valori di x compresi nell’intorno di x0, avranno sempre un’ordinata maggiore di M.
Definizione di limite finito per x tendente all’infinito
Diciamo che la funzione f(x) ha limite l per x tendente a +∞ e scriviamo:
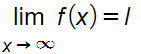
Preso un δ>0, esiste in corrispondenza un numero H>0, tale che se:
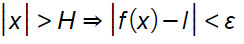
Possiamo scrivere in linguaggio formale matematico:
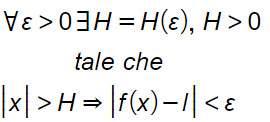
Definizione di limite infinito con x che tende a infinito
Si dice che la funzione f(x) tende all’infinito per x tendente all’infinito e si scrive:
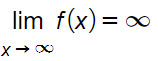
se preso un M>0, esiste in corrispondenza un H>0, funzione di M, tale che:
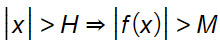
Analizzando la definizione topologica di limite, possiamo scrivere:
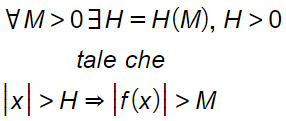
Conclusioni
In maniera del tutto analoga a quanto visto in questa lezione, è possibile individuare il limite destro e sinistro di una funzione.
Invitiamo i nostri studenti a non preoccuparsi eccessivamente delle definizioni date in questa lezione. Queste infatti sono importanti e possono essere chieste durante un’interrogazione, ma gli esercizi si risolvono con delle tecniche precisi e più semplici, come vedremo nel dettaglio nelle prossime lezioni.
Vuoi saperne di più? Vai all’indice delle lezioni sullo studio dei limiti in matematica.