Come si trova il dominio di un logaritmo? Ho un esercizio da risolvere in cui all’interno c’è un logaritmo e non so come calcolare il dominio. C’è una regola da seguire? Potreste mostrarmi quali sono i casi che si possono incontrare negli esercizi? Grazie – Sara.
Soluzione
Il dominio del logaritmo si calcola imponendo:
- argomento del logaritmo maggiore di 0;
- base del logaritmo maggiore di 0 e diversa da 1;
Nella quasi totalità dei casi, la base del logaritmo è un numero naturale, per cui l’unica regola da seguire per il calcolo del campo di esistenza è che l’argomento f(x) deve essere maggiore di 0.

Dominio del logaritmo naturale
Il Logaritmo naturale è un normale logaritmo che ha alla base la lettera e (detta Numero di Nepero). In questi casi si segue alla lettera la regola che abbiamo sopra esposto: si impone l’argomento maggiore di 0. Facciamo subito un esempio:
y=log(x²+2x)
Dominio del logaritmo: x²+2x>0. Abbiamo quindi ottenuto una disequazione di secondo grado che andiamo a risolvere.
x>0
x+2>0 → x>-2
La soluzione finale sarà x<-2 U x>0
NOTE: alcuni studenti ci chiedono come si calcola il dominio del logaritmo a base 1/2. In questo caso non cambia assolutamente nulla. Nelle condizioni iniziali abbiamo infatti esplicitato che la base deve essere maggiore di 0 e diversa da 1. Essendo questo il nostro caso, ci è sufficiente imporre l’argomento del logaritmo maggiore di 0.
Dominio logaritmo fratto
L’esercizio diventa leggermente più difficile quando si ha a che fare con il dominio di un logaritmo fratto. La regole però è sempre la stessa: l’argomento della funzione logaritmica deve essere maggiore di zero. Vediamo con un esempio come si risolve questo caso specifico.
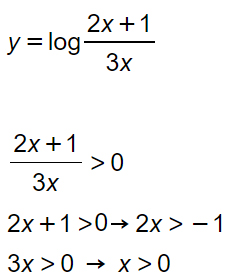
Come puoi vedere, appena si impone la condizione del dominio del logaritmo fratto, si ha di fronte una semplice disequazione fratta di primo grado. Quindi si impone numeratore maggiore di 0 e il denominatore maggiore di 0. Si procede calcolando il falso sistema e si ottengono le soluzioni.
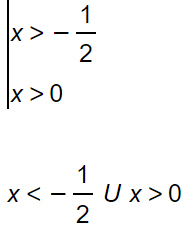
Dominio del logaritmo al denominatore
Nel caso in cui anche il logaritmo si trova al denominatore, l’esercizio si semplifica anche se bisogna ricordarsi di imporre la condizione di esistenza “denominatore diverso da 0”. Vediamo un esercizio svolto per essere più chiari.

In questo caso le due condizioni devono valere contemporaneamente, per cui si crea un sistema con una parentesi graffa. La prima riga non è altro che un’equazione logaritmica. Ricordi come si risolve? Si trasforma l’equazione ponendo tutto all’esponente con base e. Il secondo rigo è invece una disequazione di primo grado.
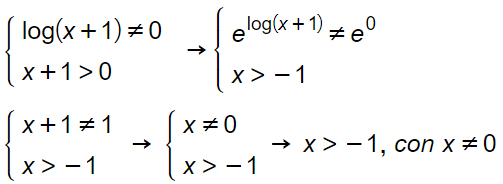
Dominio logaritmo sotto radice
Come accadeva con le funzioni fratte, l’introduzione della radice quadrata può complicare leggermente lo svolgimento dell’esercizio. Tuttavia non è il caso di spaventarsi. Ecco come si calcola il dominio di un logaritmo con la radice. Esempio svolto:

Il primo passo da fare è riconoscere quali sono gli elementi che contribuiscono a restringere il campo di esistenza: il logaritmo e la radice quadrata. Quindi andiamo ad imporre il radicando (cioè tutto ciò che è sotto la radice) maggiore e uguale di 0. Assieme a questa condizione associamo che l’argomento del logaritmo deve essere maggiore di 0.
La prima è una disequazione logaritmica. Ricordi come si risolvono? Si trasforma il logaritmo in esponente con base e e si fa qualche semplificazione. Al secondo rigo invece una banale disequazione di I grado. Ovviamente le due condizioni devono essere valide contemporaneamente, per cui si impone un sistema con la parentesi graffa.
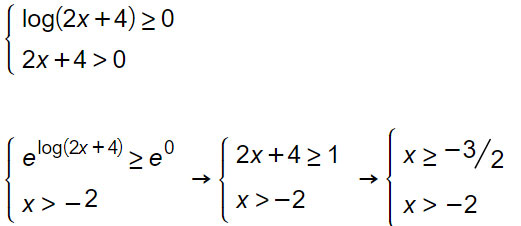
Unendo le due soluzioni, si arriva alla fine dell’esercizio:
x>-2.
Conclusioni
In questa lezione abbiamo visto come si calcola il dominio di un logaritmo in tutti i vari casi. Abbiamo visto che, sostanzialmente, l’unica vera novità quando si risolve una funzione logaritmica è quella di imporre l’argomento maggiore di zero.
Se hai trovato la lezione chiara, lascia un commento positivo. Ci aiuterà a crescere e ad offrirti ogni giorno lezioni gratuite scritte dai nostri docenti. Se invece hai ancora dei dubbi o necessiti di chiarimenti, scrivici qual è il tuo problema e cercheremo di aiutarti.
Lezione chiara e semplice complimenti.