Asintoto verticale – definizione, formula ed esempi

L’asintoto verticale è una retta verticale che indica l’andamento tendenziale della funzione in corrispondenza di un intorno x₀, generalmente non definito dal dominio. Tra i vari tipi di asintoti, quello verticale è il più facile da individuare e può essere sinistro, destro o bilatero.

In questa lezione vedremo come si trovano gli asintoti verticali, analizzando non solo le formule di calcolo da usare, ma anche le definizioni. Nella seconda parte invece ci concentreremo su alcuni esempi pratici ed esercizi svolti.

Definizione asintoto verticale

Sia f(x) una funzione definita in un sottoinsieme di R e sia x₀ un punto di accumulazione del dominio. Allora se vale la relazione:

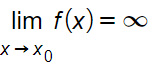
la retta di equazione x=x₀ è un asintoto verticale.

Alcuni chiarimenti

In poche parole quando la funzione si avvicina ad un punto finito sull’asse delle x, la sua y tende a più infinito o meno infinito. Nello studio di funzione generalmente si effettua il calcolo del limite sia sinistro che destro in quell’interno.

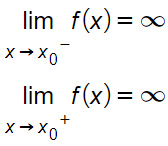
Nel primo caso si parla di asintoto verticale sinistro, nel secondo caso, quando invece il limite viene da destra, si parla di asintoto verticale destro. Nel caso in cui siano verificate entrambi i limiti, allora si parla di asintoto verticale bilatero.

OSSERVAZIONE

Si sottolinea che non necessariamente il limite destro e sinistro devono tendere allo stesso infinito. In tantissimi esercizi capiterà che il limite destro tenda a più infinito mentre quello sinistro a meno infinito (o viceversa). Ciò non viola la definizione data, per cui saremo ancora in presenta di rette asintotiche verticali.

Calcolo asintoto verticale

Come si procede in genere per trovare gli asintoti verticali di una funzione?

• Si effettua lo studio del dominio della funzione e si trovano eventuali punti di discontinuità. Nelle razionali fratte, ad esempio, imponendo il denominatore diverso da zero, si otterrà un risultato del tipo x≠x₀. E’ proprio quest’ultimo valore che inseriremo all’interno dei limiti verticali.
• Si calcolano il limite destro e sinistro della funzione attorno al punto x₀. Se i limiti tendono a ±∞, allora la retta x=x₀ è un asintoto orizzontale.

La differenza con gli altri asintoti

Rispetto all’asintoto orizzontale o all’asintoto obliquo, in questo caso la ricerca del limite non avviene su valori infiniti. Nei casi precedenti eravamo abituati a studiare il limite della funzione per x che tende a infinito. In questo caso invece il limite va studiato in corrispondenza di un valore finito.

Asintoto verticale esempi

Quando una funzione presenta un asintoto verticale è sempre possibile stabilire con esattezza l’andamento del suo grafico in prossimità dell’asintoto calcolando i limiti destro e sinistro. In particolare sono possibili quattro casi:

Caso 1

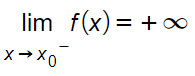
Se x tende a x₀ da sinistra, le ordinate dei punti delle funzioni tenderanno sempre più a +∞. Quindi sul grafico la curva tende ad andare verso l’alto.

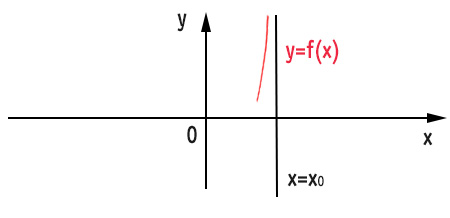
Caso 2

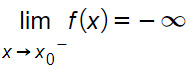
Per x che tende a x₀ da sinistra, le ordinate dei punti appartenenti alla funzione tendono a -∞, per cui sul grafico la funzione si sposta sempre più verso il basso.

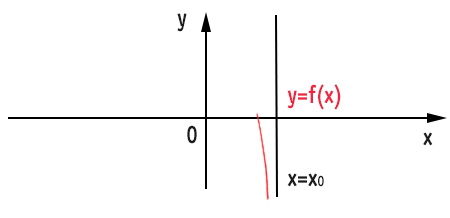
Caso 3

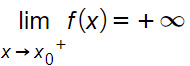
Quando x tende a x₀ da destra, le ordinate della funzione f(x) si avvicinano sempre di più a +∞. Questo vuol dire che la curva sul grafico parte dall’alto e si abbassa velocemente.

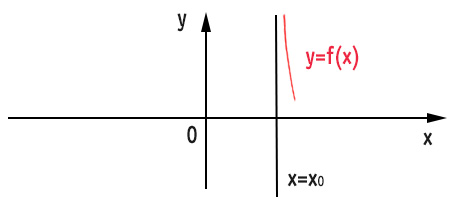
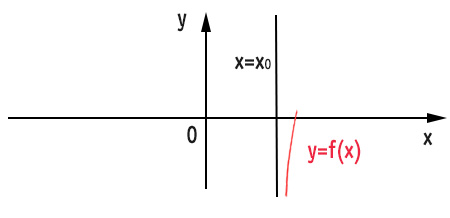
Caso 4

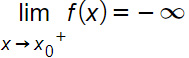
Quando x tende a x₀ da destra, le ordinate della funzione tendono sempre più a meno infinito. Questo vuol dire che il grafico della funzione parte dal basso e cresce molto velocemente spostandosi verso destra.

Esercizi svolti

Trovare gli asintoti verticali della seguente funzione:

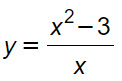
Svolgimento

Poiché la funzione è una razionale fratta, il dominio è:

D: x≠0

Si tratta di un dominio illimitato, visto che può andare sia a più che a meno infinito. C’è un punto singolare che genera la discontinuità. Può avere quindi un asintoto verticale. Per capirlo, calcoliamo il limite della funzione per x che tende a 0, sia da destra che da sinistra.

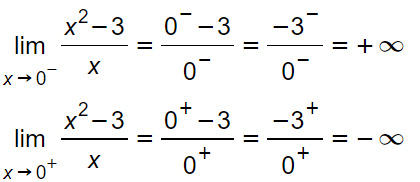
Poiché il limite nel punto 0 va a infinito, allora:

x=0 è un asintoto verticale.

Possiamo quindi rappresentare sul grafico, l’andamento della curva.

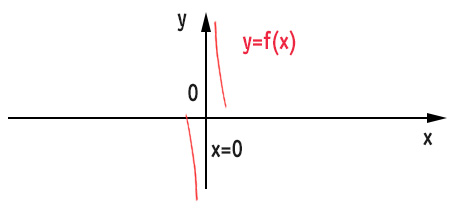
Da notare come a sinistra della retta x=0 (che coincide con l’asse delle ordinate), la curva tenda a meno infinito, mentre a destra di x=0 la funzione tende a più infinito.