Quali sono gli angoli complementari? Quali caratteristiche hanno? Che vuol dire quando la traccia di un esercizio parla di un angolo complementare?
In questa lezione vedremo quando due angoli si dicono complementari e come si risolvono gli esercizi sia per le scuole medie che superiori. Iniziamo subito dal significato del termine.
Che significa angolo complementare? La parola deriva da “complemento” e sta ad indicare un’aggiunta a qualcosa.
Angoli complementari definizione
Dati due angoli α eβ, questi si dicono complementari quando la loro somma è pari ad un angolo retto.
Poiché quest’ultimo misura 90°, possiamo anche dire che due angoli sono complementari quando la loro somma è pari a 90°.
Esempio
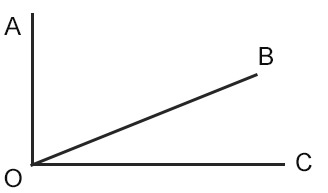
Nella figura, possiamo notare la somma di due angoli:
AOB+BOC=AOC
Poiché proprio AOC è un angolo retto, allora vuol dire che:
AOB+BOC=90°
Quindi AOB e BOC sono due angoli complementari.
Proprietà e caratteristiche
- Due angoli complementari sono necessariamente acuti.
- Il triangolo rettangolo si definisce così perché ha un angolo retto e due angoli tra loro complementari.
- Si parla di angolo complementare rispetto ad un altro quando la sua ampiezza è pari a 90° meno il primo angolo.
Su quest’ultimo punto dedichiamo più attenzioni con un esercizio specifico. La parte teorica è già conclusa. Facciamo qualche esercizio assieme ora…
Esercizi sugli angoli complementari
Esercizio 1
Calcola la misura dell’angolo complementare all’angolo 47°28′.
Svolgimento
Abbiamo affrontato un esercizio molto simile nella lezione sugli angoli supplementari. In questo caso la traccia ci chiede di calcolare un angolo che, sommato a quello noto di 47° 28′, ci dà proprio 90°.
Detto α l’angolo da calcolare, possiamo scrivere che:
α+47°28’=90° → α = 90° – 47°28′
Mettiamo in colonna gli angoli svolgendo una semplice sottrazione. Ricordati che gli angoli seguono il sistema sessagesimale, per cui 1 grado è uguale a 60 primi.
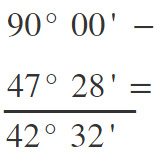
Esercizio 2
La differenza di due angoli complementari è 16°. Determinare la misura dei due angoli.
Svolgimento
Gli studenti delle scuole superiori possono scrivere un sistema di primo grado in cui le due equazioni sono x+y=90° e x-y=16°. Si hanno così due equazioni in due incognite.
Per gli studenti delle scuole medie proviamo a ragionare in maniera diversa. Immaginiamo di disegnare la misura dei due angoli come se fossero due segmenti.
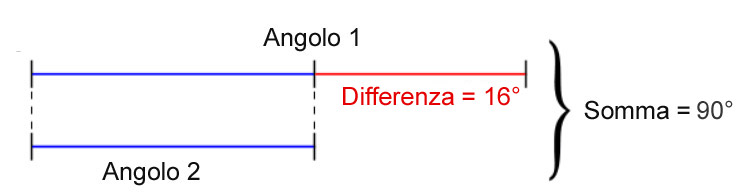
Da notare che se alla somma sottraiamo la differenza ci restano i due segmenti blu, tra loro uguali. Per cui possiamo scrivere che:
90°-16°=2β
β=74°:2=37°
Poiché infine α è il complementare di β, possiamo trovare la soluzione:
α=90°-37°
α=53°
Esercizio 3
Calcolare l’ampiezza di due angoli complementari, sapendo che il primo è il triplo del secondo.
Svolgimento
Anche in questo caso gli studenti delle scuole superiori possono sfruttare le equazioni di primo grado e scrivere un semplice sistema a due incognite dove le equazioni sono x+y=90° e x=3y
Per gli studenti delle scuole medie, invece ragioniamo ancora con i segmenti unitari. Sapendo che il primo è il triplo del secondo, vuol dire che possiamo considerare il più piccolo come 1 segmento e quello più grande come 3 segmenti.
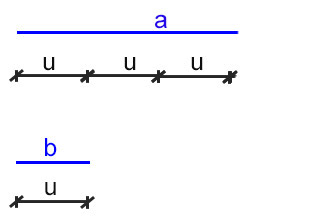
Quindi in totale ci sono 4 segmenti u la cui somma è 90°. Possiamo quindi scrivere che:
4u=90° → u=22,5° → u=22° 30′
β=22° 30′
Ricordando che 0,5° sono pari a 0,5 per 60 primi, cioè 30′, non ci resta che calcolare l’angolo complementare. Si procede quindi esattamente come nell’esercizio 1 già visto sopra.
α=90°-22° 30′ = 67° 30′
Conclusioni
Gli esercizi su angoli complementari e supplementari sono molto simili dal punto di vista del metodo. L’unica cosa che cambia è il valore della somma.
Nel primo caso, sommando i due angoli, si ottiene 90°, mentre nel secondo caso si ottiene 180°.