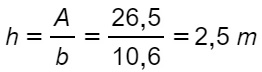In questa lezione vedremo un approfondimento specifico sull’altezza del parallelogramma. Analizzeremo le formule (o meglio le formule inverse) da usare e cercheremo di applicarle ad alcuni semplici esercizi.
Definizione e figura
Prima di vedere come si calcola l’altezza di un parallelogramma, vediamo come si disegna e che cos’è.
Approfondimento: consulta tutte le formule sul parallelogramma
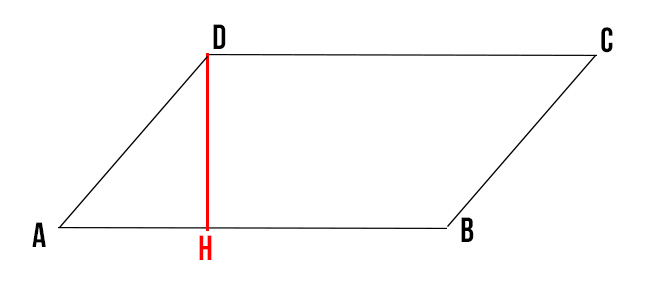
Il segmento DH in figura è l’altezza del parallelogramma relativa alla base AB. Dalle nozioni generali di geometria sappiamo che l’altezza è il segmento che congiunge perpendicolarmente il vertice di un poligono con il lato opposto.
Come calcolare l’altezza del parallelogramma
L’unica formula che permette di calcolare direttamente l’altezza di questa figura geometrica è quella dell’area del parallelogramma. In particolare bisogna determinare la formula inversa.
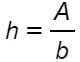
Caratteristiche e proprietà
Questa seconda parte è importante perché ti mostreremo dei modi alternativi per calcolare l’altezza di un parallelogramma.
Innanzitutto possiamo notare che l’altezza divide la figura in un triangolo rettangolo e in un trapezio rettangolo. Questo significa che l’altezza del parallelogramma è anche uno dei cateti del triangolo e l’altezza del trapezio.
Quindi potremo utilizzare il teorema di Pitagora nei vari esercizi e le formule del trapezio.
Parallelogramma altezza – esercizi svolti
Esercizio 1
In un parallelogramma l’altezza misura 2,25 m e l’area è
di 5,31 m². Calcola la misura della base del parallelogramma.
Svolgimento
Il primo esercizio che svolgiamo assieme si fornisce area e altezza. Basta quindi provare la formula inversa dell’area per calcolarne la base.
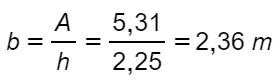
Esercizio 2
In un parallelogramma la base misura 10,6 m e l’area è di 16,5 m². Calcola la misura dell’altezza del parallelogramma.
Svolgimento
L’esercizio è perfettamente analogo al precedente, ma questa volta l’incognita da calcolare è proprio l’altezza del parallelogramma. Uso quindi la formula inversa ed ottengo immediatamente la soluzione.