Abbiamo già affrontato la definizione di funzione matematica generica, vedendo i grafici, insiemi ed esempi concreti. In questa lezione completeremo l’argomento parlando di funzione iniettiva, suriettiva e biettiva. Non aver paura, non è niente di particolarmente difficile da capire e anche se a scuola non ci hai capito nulla, vedrai che al termine di questa lezione avrai tutto molto più chiaro.
Ci concentreremo su ciascuna di queste vedendo qual è la definizione e come può essere spiegata in maniera semplice attraverso l’uso di un grafico. La prima domanda che sicuramente ti stai ponendo è: “a che servono le funzioni iniettive e suriettive?“. Nel programma di analisi ti troverai spesso a sentir parlare di funzioni inverse e invertibili. Tutto parte dai contenuti che affronteremo in maniera semplice e schematica nella lezione di oggi.
Funzioni iniettive
Iniziamo subito con la definizione di funzione iniettiva così come la trovi sui libri di matematica che usi anche a scuola.
Sia f una funzione che trasforma elementi dell’insieme A in elementi dell’insieme B. Diciamo che f è una funzione iniettiva tra gli insiemi A e B se gli elementi di B posseggono al massimo una controimmagine.
Per capire quando una funzione si dice iniettiva basta che ricordi la definizione di funzione. Dicemmo che è una relazione che associa per ogni elemento di A uno e un solo elemento di B. Le funzioni iniettive hanno la caratteristica per cui anche agli elementi di B corrisponde un solo elemento dell’insieme A.
Ti facciamo notare come possano esistere degli elementi dell’insieme B privi di controimmagine (cioè di elementi collegati nell’insieme A)
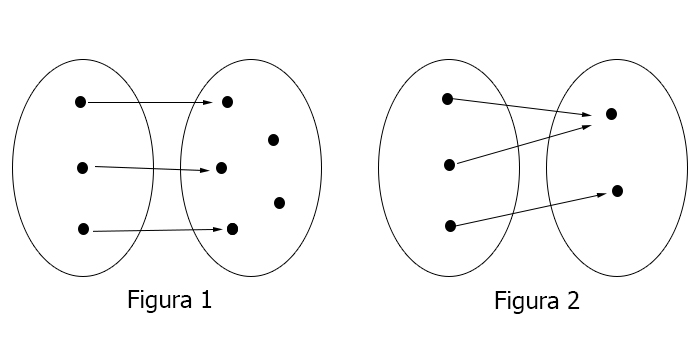
Funzione iniettiva grafico
Nell’immagine la figura 1 è una funzione iniettiva, mentre la figura 2 non è una funzione iniettiva. Questo perché nel grafico a destra puoi vedere che alcuni elementi dell’insieme a sinistra convergono verso un’unico elemento dell’insieme di destra, condizione non accettabile per la definizione.
Esempi
Esercizio 1 – Dimostrare che y=1/x è una funzione iniettiva
Per verificare che la funzione assegnataci dalla traccia sia iniettiva occorre verifica che non solo passando da x a y (quindi dall’insieme A a quello B) c’è un solo collegamento per ogni elemento, ma deve valere anche il contrario. Per ogni elemento di y deve corrispondere 1 solo elemento di x.
Possiamo farlo andando a calcolare x=1/y. Assegniamo dei valori arbitrari (cioè a nostra scelta) alla y, tranne 0 perché non rientra nel dominio delle funzioni fratte.
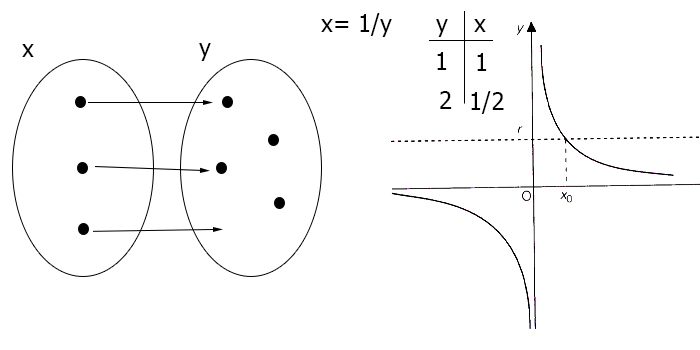
Funzione iniettiva esempio
Dal grafico della funzione sul piano cartesiano puoi anche notare che per qualsiasi retta r orizzontale (tratteggiata in figura) ci sarà un solo punto di intersezione con curva. Questo significa che ogni valore dell’insieme B, come ad esempio il valore sull’asse delle y pari a r (y=r retta orizzontale) ha una sola controimmagine. Infatti puoi vedere che in corrispondenza di r esiste un solo valore sull’asse delle ascisse, pari a x0.
Esercizio 2 – Verificare che la traccia esprima una funzione iniettiva.
y=(1-x)/(1+x), dove la funzione è definita per l’insieme numerico Z (numeri interi relativi). Il dominio della funzione è l’insieme Z ed inoltre x deve essere diverso da -1.
Il codominio C della funzione è strettamente contenuto in Q, poiché si possono individuare gli elementi di Q privi di controimmagine; stabiliamo per esempio, se l’elemento 3/2 ha controimmagine:
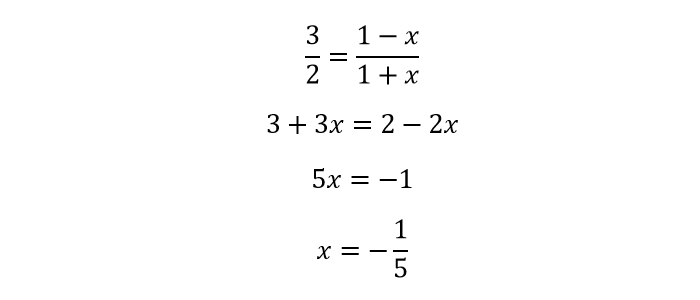
Funzioni iniettive esempio
Il valore determinato non è accettabile poiché non è un numero intero relativo, quindi 3/2 (l’elemento dell’insieme B) non ha controimmagine (cioè non vi è associato alcun elemento dell’insieme A). Abbiamo così dimostrato che quel determinato valore non ha una controimmagine.
Quello che ci resta da stabilire per completare questo esercizio sulle funzioni iniettive è che presi due qualsiasi numeri x1 e x2 le loro immagini sono differenti, cioè f(x1) è diverso da f(x2). Si tratta di una dimostrazione che facciamo per assurdo. Supponiamo quindi che sia:
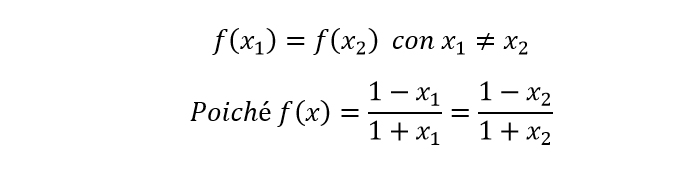
A questo punto andiamo a calcolare il minimo comune multiplo per poter proseguire con questa semplice equazione di primo grado ma a due incognite.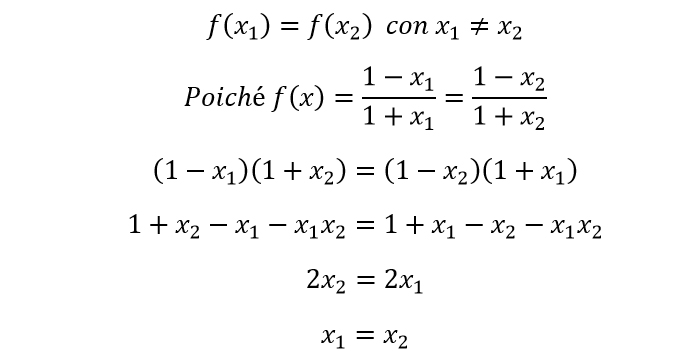
L’esercizio ci ha portato ad un risultato che contrasta con l’ipotesi iniziale (cioè che x1 diverso da x2). Dobbiamo perciò considerare che f(x1)=f(x2). Abbiamo così dimostrato che le funzione di partenza assegnataci dalla traccia è iniettiva.
In realtà l’esercizio che ti abbiamo mostrato in questo secondo esempio è ben più complesso rispetto a quelli che svolgerai in classe. Generalmente i programmi e gli esercizi di matematica che ti vengono assegnati in aula non riguardano le funzioni iniettive e suriettive su cui invece ti limiterai all’enunciato e ad una rapida spiegazione con gli insiemi. Dovrai cioè sapere quello che abbiamo studiato in questa prima parte di lezione.