Il teorema di Nepero è una formula utilizzata in trigonometria che permette di risolvere un generico triangolo nel caso in cui si conoscano le misure di due lati e dell’angolo compreso. Viene chiamato anche teorema delle tangenti perché nella formula principale compare l’uso diretto delle tangenti degli angoli.
Non capita spesso di utilizzare il teorema di Nepero, tanto che spesso viene tralasciato. Tuttavia merita un approfondimento, seppure breve, almeno per valutarne formula e potenzialità. Il nome di questa teorie viene dal matematico Nepero, lo stesso che formulò quello che oggi viene appunto chiamato numero di Nepero, fondamentale nello studio dei logaritmi.
Formula del teorema di Nepero
Per prima cosa disegniamo un generico triangolo (quindi un triangolo scaleno) in cui andiamo ad indicare l’ampiezza degli angoli e la misura dei lati.
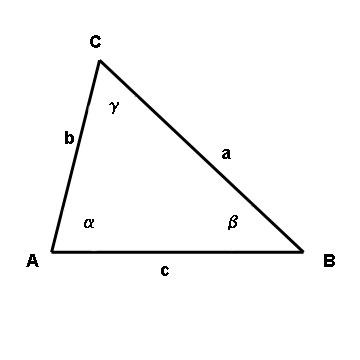
Enunciato
In ogni triangolo, la somma di due lati sta alla loro differenza come la tangente della semisomma degli angoli opposti sta alla tangente della loro semidifferenza.
(oppure)
In ogni triangolo rettangolo la somma di due lati sta alla loro differenza come la cotangente della metà dell’angolo compreso sta alla tangente della semidifferenza degli angoli opposti.
Formule
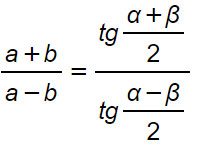
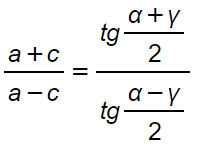
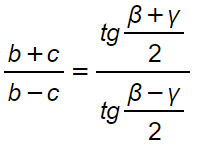
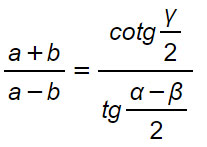
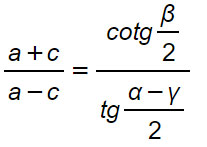
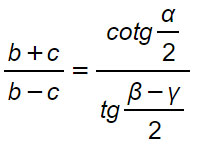
Considerazioni sul teorema di Nepero
Dato si tratta di formule non molto utilizzate, ne tralasciamo la dimostrazione. Facciamo invece alcune considerazioni di carattere pratico. Quando si usa questo teorema negli esercizi di trigonometria?
- quando è noto un lato e due angoli
- quando sono noti due lati e l’angolo compreso
Perché il teorema delle tangenti viene usato poco? Perché sostanzialmente non permette di arrivare sempre ad una soluzione semplice. Può capitare infatti che porti a calcolare la tangente della somma di due angoli, di cui magari uno è incognito. Per questa ragione si preferisce in genere sfruttare molto più facilmente e rapidamente il teorema del seno.